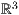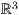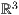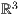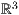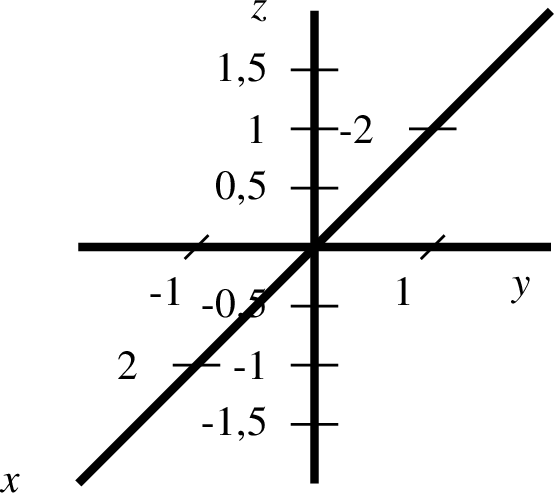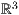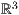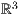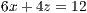8 Dreidimensionale Abbildungen
- Die Parallelprojektion
- Zeichenbefehle für den
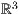
- Koordinatensysteme und Gitter im
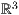
- Plotten von Funktionen und Daten im
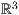
- Objekte für die analytische Geometrie
- Körper im
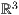
Für die Oberstufenmathematik benötigt man in der Analytischen Geometrie einige
dreidimensionalen Zeichenelemente. So habe ich mein Skript auf mehrere
Elemente im 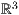 erweitert. Ich habe mich bemüht so viele Zeichenroutinen
wie möglich in den
erweitert. Ich habe mich bemüht so viele Zeichenroutinen
wie möglich in den 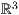 zu übertragen, aber aus Zeitmangel ist diese
Übertragung noch nicht vollständig. Die Zeichenelemente werden dabei durch die
Parallelprojektion in die Bildebene transformiert.
zu übertragen, aber aus Zeitmangel ist diese
Übertragung noch nicht vollständig. Die Zeichenelemente werden dabei durch die
Parallelprojektion in die Bildebene transformiert.
8.1 Die Parallelprojektion
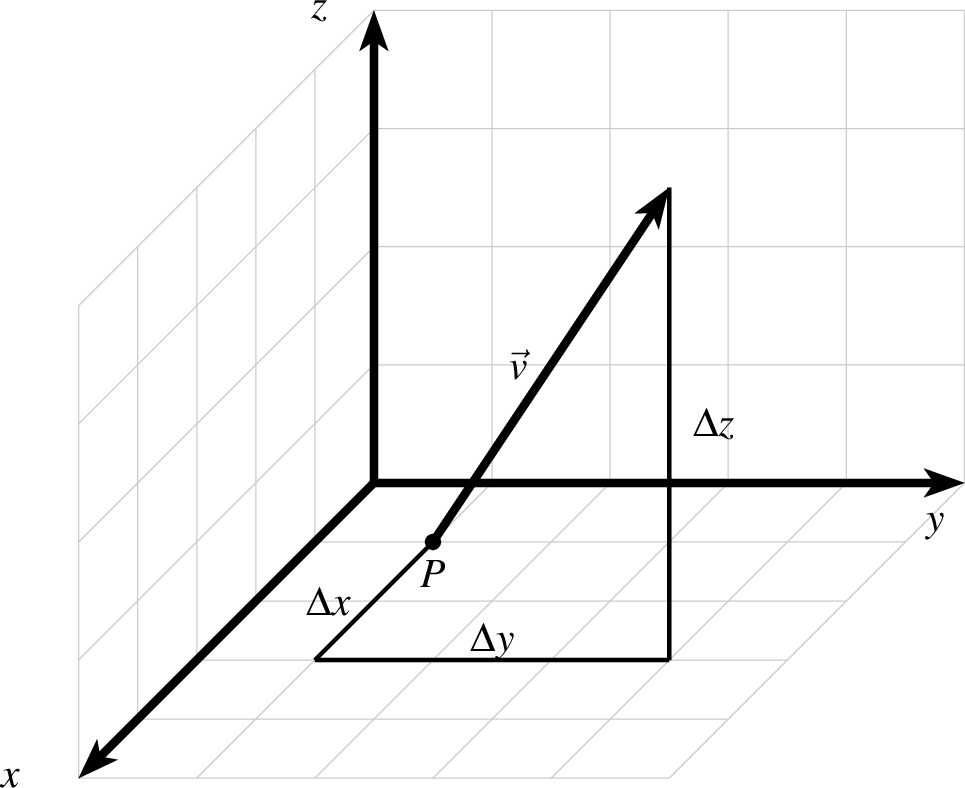
In der Abbildung 8.1 sieht man einen dreidimensionalen Punkt
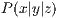 im Koordinatensystem
im Koordinatensystem 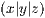 , der mithilfe der Parallelprojektion
in den Punkt
, der mithilfe der Parallelprojektion
in den Punkt 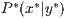 im System
im System 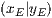 verwandelt wird. Der Winkel
verwandelt wird. Der Winkel
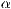 stellt dabei die horizontale Rotation quer zu
stellt dabei die horizontale Rotation quer zu  -Achse dar. Der
Winkel
-Achse dar. Der
Winkel 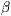 ist die vertikale Rotation, bezogen auf die Papierebene.
Die Transformation ist dabei die folgende:
ist die vertikale Rotation, bezogen auf die Papierebene.
Die Transformation ist dabei die folgende:
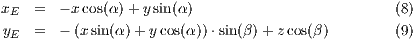
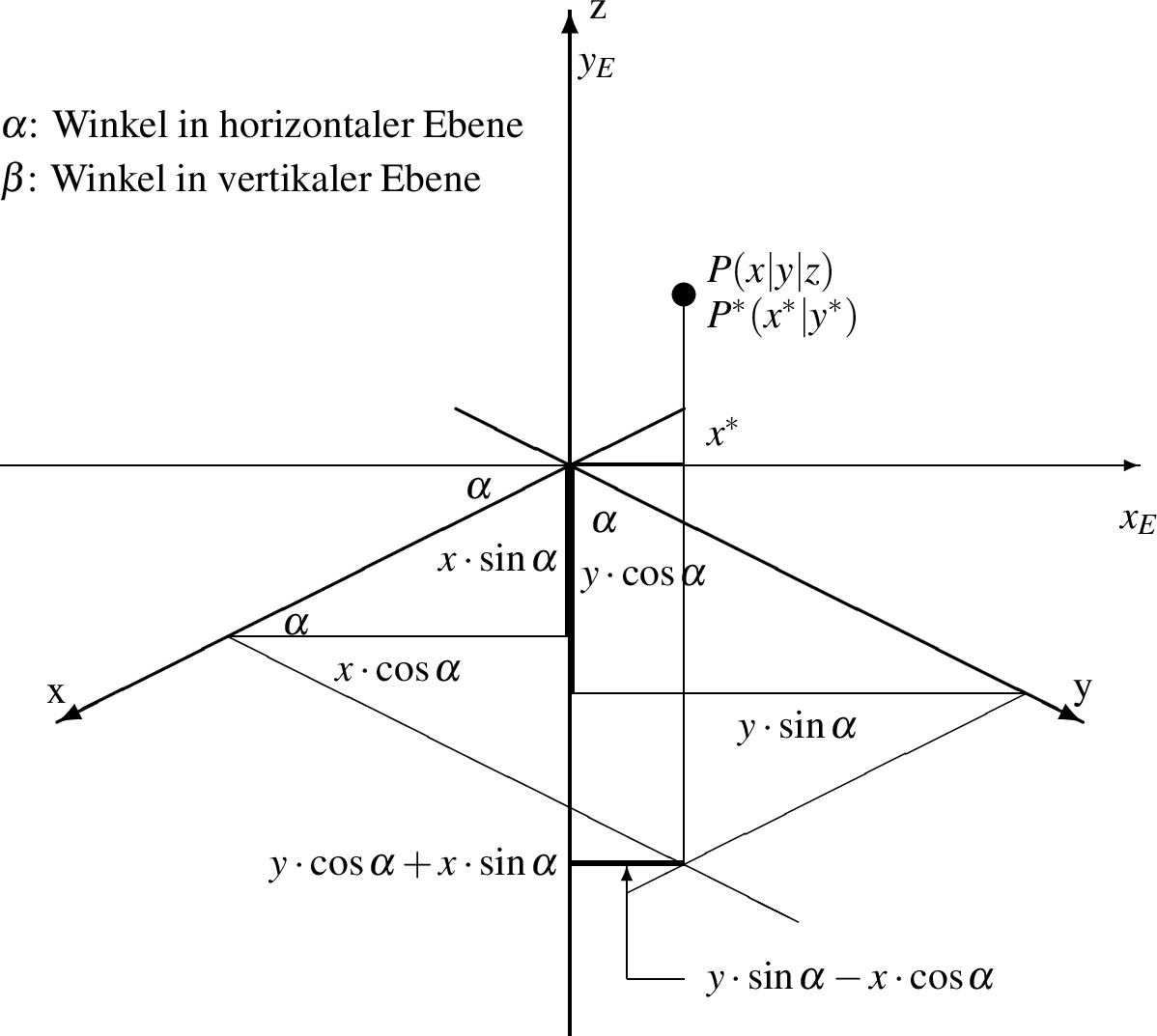
Abb. 130: Koordinaten in einem dreidimensionalen Koordinatensystem (aus : [Voß, 2008, S. 355] )
Diese Winkel kann man dabei mit dem Befehl einstellung global
setzen.
einstellung
[layer=< 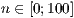 >]
>]
[alpha=<Winkel in Grad>]
[beta=<Winkel in Grad>]
[coortype=<0|1|2|3>]
[pstricks]
Dabei ist alpha auf 45, beta auf 30 und coortype
auf 2 gesetzt. Ist pstricks gesetzt, so werden alle Elemente mit dem
pst-3plot-Paket1 aus
PsTricks gesetzt. Ansonsten werden alle Zeichenelemente intern transformiert.
Der Befehl coortype beschreibt weitere Projektionsverfahren, die die
folgenden sind:
- coortype=0
- Die Parallelprojektion wie oben beschrieben.
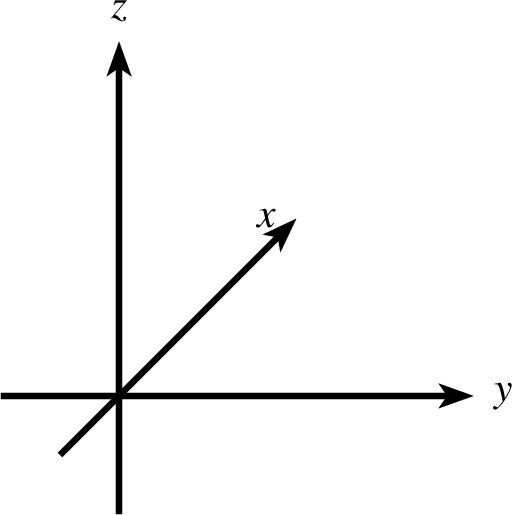
coor0-ptxt.ptxt 1 einstellung alpha=45 beta=30 coortype=0 pstricks 2 koordinatensystem x=-1,3 y=-1,3 z=-1,3 einteilung=1,1,1 skala=keine text="$x$","$y$","$z$" - coortype=1
- Die
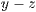 -Achsen sind orthogonal und der Winkel zwischen der
-Achsen sind orthogonal und der Winkel zwischen der
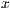 - und
- und 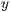 -Achse ist durch
-Achse ist durch 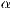 gegeben. Der Winkel
gegeben. Der Winkel 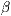 ist
bedeutungslos.
ist
bedeutungslos.
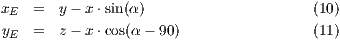
coor1-ptxt.ptxt 1 einstellung alpha=45 beta=30 coortype=1 pstricks 2 koordinatensystem x=-1,3 y=-1,3 z=-1,3 einteilung=1,1,1 skala=keine text="$x$","$y$","$z$" - coortype=2
- Die
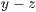 -Achsen sind orthogonal und der Winkel zwischen der
-Achsen sind orthogonal und der Winkel zwischen der
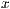 - und
- und 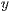 -Achse ist
-Achse ist 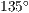 und die
und die 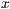 -Achse ist um den Wert
-Achse ist um den Wert
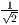 verkürzt. Die Winkel
verkürzt. Die Winkel 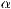 und
und 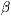 sind
bedeutungslos.
sind
bedeutungslos.

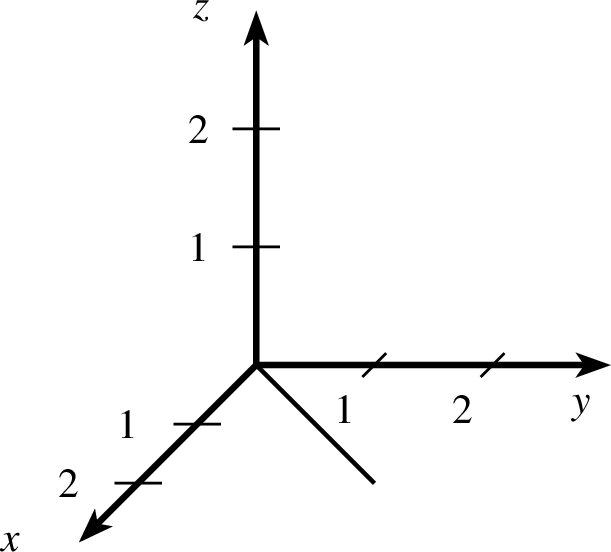
coor2-ptxt.ptxt 1 einstellung alpha=45 beta=30 coortype=2 pstricks 2 koordinatensystem x=-1,3 y=-1,3 z=-1,3 einteilung=1,1,1 skala=keine text="$x$","$y$","$z$" - coortype=3
- Die
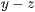 -Achsen sind orthogonal und der Winkel zwischen der
-Achsen sind orthogonal und der Winkel zwischen der
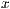 - und
- und 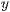 -Achse ist
-Achse ist 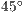 und die
und die 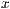 -Achse ist um den Wert
-Achse ist um den Wert
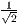 verkürzt. Die Winkel
verkürzt. Die Winkel 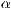 und
und 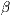 sind
bedeutungslos.
sind
bedeutungslos.

coor3-ptxt.ptxt 1 einstellung alpha=45 beta=30 coortype=3 pstricks 2 koordinatensystem x=-1,3 y=-1,3 z=-1,3 einteilung=1,1,1 skala=keine text="$x$","$y$","$z$"
8.2 Zeichenbefehle für den 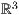
8.2.1 Linien, Vektoren und Polygone
Linien zeichnen
Auch im 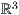 werden viele Zeichenobjekten aus Linien aufgebaut. So ist die
Linie erweitert worden:
werden viele Zeichenobjekten aus Linien aufgebaut. So ist die
Linie erweitert worden:
linie
[layer=< 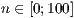 >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt ( 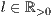 )>,<Linienart>[,"<Pfeiltyp>"]]
)>,<Linienart>[,"<Pfeiltyp>"]]
[parameter="<Pstricksbefehle>"]
p=< 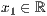 >,<
>,< 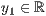 >,<
>,< 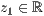 >
>
p=< 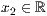 >,<
>,< 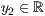 >,<
>,< 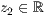 >
>
[text="<Text>"[,<Textdrehwinkel in Grad>,<Textausrichtung>,< 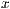 -Richtung>,<
-Richtung>,< 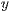 -Richtung>],<
-Richtung>],<  -Richtung>]
-Richtung>]
In p stehen die Koordinaten des Anfangs und Endpunktes der
Linie. Zusätzlich kann noch ein Text mit text an die Linie
geschrieben werdenmit dem Befehl text, der optional
ist. Wird nur ein Text für sich gesetzt, so wird der mittig von
der Linie platziert.
| linie-3d-ptxt.ptxt |
|---|
| 1 koordinatensystem x=0,3 y=0,3 z=0,3 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 2 linie farbe=black linie=1,solid p=0,0,0 p=2,2,0 |
| linie-3d-2-ptxt.ptxt |
|---|
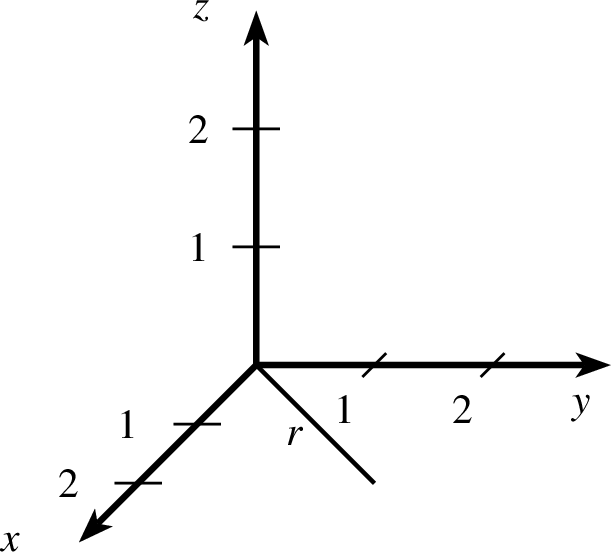
| 1 koordinatensystem x=0,3 y=0,3 z=0,3 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 2 linie farbe=black linie=1,solid p=0,0,0 p=2,2,0 text="$r$",0,180,0.2,0,0 |
| linie-3d-3-ptxt.ptxt |
|---|
| 1 koordinatensystem x=0,3 y=0,3 z=0,3 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 2 linie farbe=red linie=1,solid 3 0,0,0 4 1,0,2 5 0,2,1 6 2,2,0 7 ende |
Linien mit Verschiebungen
Ein neuer Befehl ist der Linienbefehl vlinie. Bei diesem gibt man
von einem Startpunkt die Verschiebung in 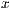 -,
-, 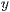 - und
- und  -Richtung an.
-Richtung an.
vlinie
[layer=< 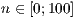 >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt ( 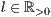 )>,<Linienart>[,"<Pfeiltyp>"]]
)>,<Linienart>[,"<Pfeiltyp>"]]
[parameter="<Pstricksbefehle>"]
p=< 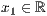 >,<
>,< 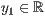 >,<
>,< 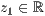 > r=<
> r=< 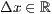 >,<
>,< 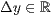 >,<
>,< 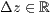 >
>
[text="<Text>"[,<Drehwinkel des Textes in Grad>,<Textausrichtung>,< 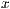 -Richtung>,<
-Richtung>,< 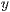 -Richtung>]]
-Richtung>]]
| vlinie-3d-ptxt.ptxt |
|---|
| 1 einstellung pstricks 2 koordinatensystem x=-1,3 y=-1,3 z=-1,3 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 3 vlinie linie=1,solid,"|->" p=2,3,0 r=2,-1,1 text="$r$",0,180,0.2,0,0 4 vlinie farbe=black linie=1,solid,"|->" p=1,1,0 r=2,1,3 text="$a$" |
Vektoren zeichnen
Vektoren kann man natürlich wie unter 4.1.2 bereits im 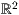 beschrieben zeichnen, indem man den pfeiltyp auf
beschrieben zeichnen, indem man den pfeiltyp auf "->" setzt. Dies
erledigt allerdings auch schon der Befehl vektor selbst, der analog
zum Befehl der Linie ist.
| vektor-3d-ptxt.ptxt |
|---|
| 1 koordinatensystem x=0,3 y=0,3 z=0,3 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 2 vektor farbe=black linie=1,solid p=0,0,0 p=2,2,0 |
Polygonzüge im 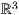 zeichnen
zeichnen
Möchte man anstelle von aneinandergereihten Linien einen geschlossen
Polygonzug zeichnen, so nutzt man den Befehl polygon wie im 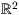 ,
der fast ähnlich zum Linienbefehl aussieht. Zusätzlich zu der Linienfarbe kann
mit farbe die Linienfarbe und Füllfarbe definiert
werden.
,
der fast ähnlich zum Linienbefehl aussieht. Zusätzlich zu der Linienfarbe kann
mit farbe die Linienfarbe und Füllfarbe definiert
werden.
polygon
[layer=< 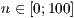 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 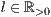 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
[lese <Dateiname>] oder [< 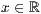 >,<
>,< 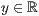 >,<
>,< 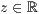 >] beliebig oft
>] beliebig oft
ende
| polygon-3d-ptxt.ptxt |
|---|
| 1 koordinatensystem x=0,3 y=0,3 z=0,3 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 2 polygon farbe=blue,solid,blue!20 linie=1,solid,blue parameter="" 3 0,0,0 4 1,1,2 5 0,1,2 6 2,2,0 7 ende |
8.2.2 Dreiecke und Vierecke im 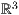 zeichnen
zeichnen
Dreiecke
Wie im 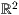 gibt es auch hier den Befehl des Dreiecks, der analog zum Befehl
unter Abschnitt 4.2.1 ist.
Die Syntax ist nur um die
gibt es auch hier den Befehl des Dreiecks, der analog zum Befehl
unter Abschnitt 4.2.1 ist.
Die Syntax ist nur um die  -Koordinate erweitert.
-Koordinate erweitert.
dreieck
[layer=< 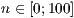 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 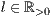 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 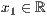 >,<
>,< 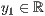 >,<
>,< 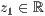 >
>
p=< 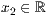 >,<
>,< 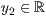 >,<
>,< 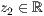 >
>
p=< 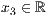 >,<
>,< 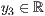 >,<
>,< 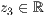 >
>
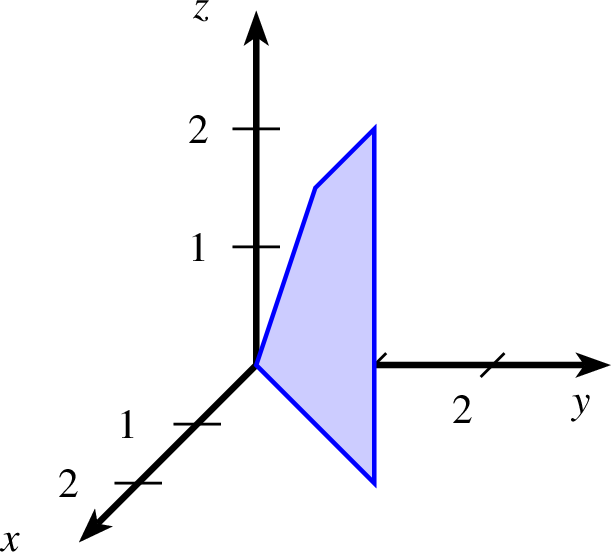
Beim Dreieck werden die Koordinanten der drei Eckpunkte angegeben.
| dreieck-3d-ptxt.ptxt |
|---|
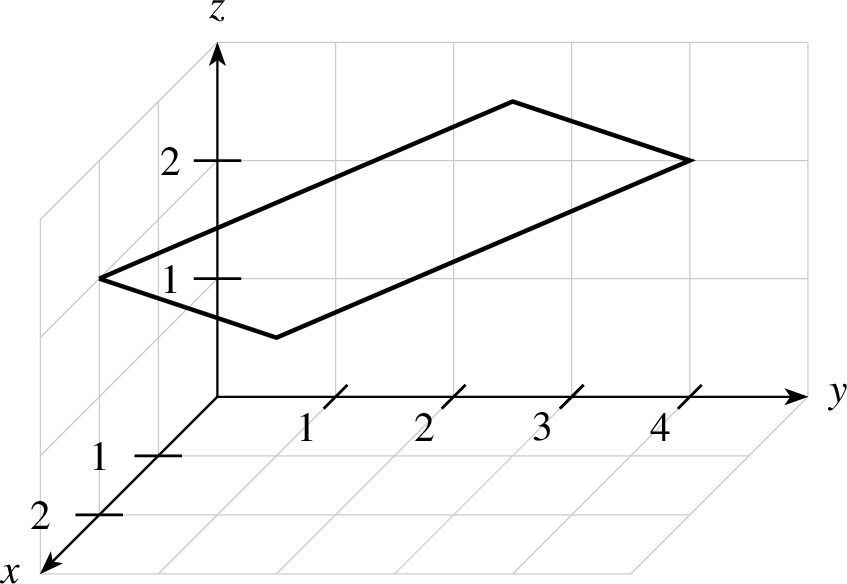
| 1 koordinatensystem x=0,3 y=0,3 z=0,2 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 2 gitter 3 dreieck farbe=black,solid,red!20 linie=1,solid parameter="opacity=0.5" p=1,0,0 p=1,1,2 p=2,3,2 |
Vierecke
Bei eineViereck übergibt man wie unter 4.2.3 an den Startwert und die drei weiteren Koordinaten im 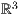 .
.
viereck
[layer=< 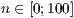 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 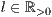 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 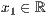 >,<
>,< 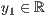 >,<
>,< 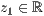 > p=<
> p=< 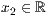 >,<
>,< 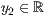 > ,<
> ,< 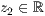 >
>
p=< 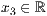 >,<
>,< 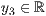 > ,<
> ,< 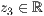 > p=<
> p=< 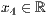 >,<
>,< 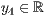 >,<
>,< 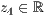 >
>
| viereck-3d-ptxt.ptxt |
|---|
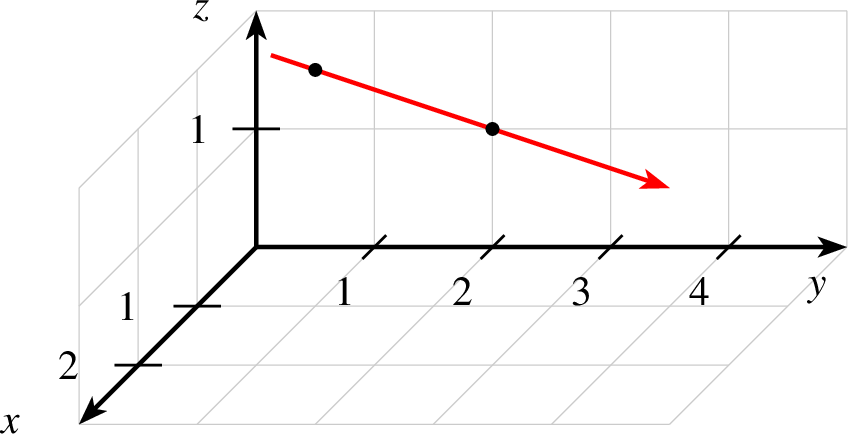
| 1 koordinatensystem x=0,3 y=0,3 z=0,3 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 2 gitter 3 viereck farbe=black,solid,red!20 linie=1,solid parameter="opacity=0.5" p=1,0,1 p=2,3,0 p=0,3,0 p=1,0,3 |
8.2.3 Ellipsen und Kreise
Ausgehend von einer Ellipse im 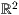 lautet die Gleichung für eine
Ellipse im
lautet die Gleichung für eine
Ellipse im 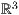
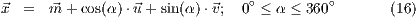
wobei 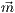 der Mittelpunkt der Ellipse ist und
der Mittelpunkt der Ellipse ist und 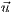 und
und 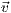 die senkrecht aufeinander stehenden Vektoren der Halbachsen
sind. Die Syntax zur Erstellung einer Ellipse ist dann
die senkrecht aufeinander stehenden Vektoren der Halbachsen
sind. Die Syntax zur Erstellung einer Ellipse ist dann
ellipse
[layer=< 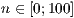 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 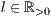 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 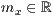 >,<
>,< 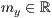 >,<
>,< 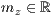 >
>
r=< 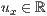 >,<
>,< 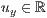 >,<
>,< 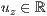 >
>
r=< 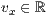 >,<
>,< 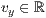 >,<
>,< 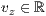 >
>
[r=<Startwinkel für 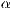 >,<Endwinkel für
>,<Endwinkel für 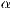 >]
>]
Standardmäßig wird die Ellipse zwischen 0 und 360 Grad gezeichnet.
Ein Kreis ist der Spezielfall der Ellipse mit 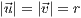 . Somit braucht man nur einen Vektor anzugeben, um einen Kreis zu zeichnen:
. Somit braucht man nur einen Vektor anzugeben, um einen Kreis zu zeichnen:
| ellipse-3d-ptxt.ptxt |
|---|
| 1 einstellung pstricks 2 koordinatensystem x=-3,3 y=-3,3 z=-2,2 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 3 ellipse farbe=black,solid,red!20 linie=1,solid,red parameter="opacity=0.5" p=0,0,0 r=0.5,-1,1 r=1,-2.25,1 4 ellipse p=2,0,0 r=1,-1,0.75 r=1,-1,1 r=0,180 |
[layer=<
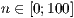 >]
>][farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (
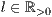 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]][parameter="<Pstricksbefehle>"]
p=<
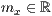 >,<
>,< 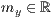 >,<
>,< 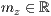 >
>r=<
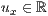 >,<
>,< 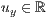 >,<
>,< 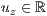 >
>[r=<Startwinkel für
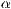 >,<Endwinkel für
>,<Endwinkel für 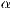 >]
>]
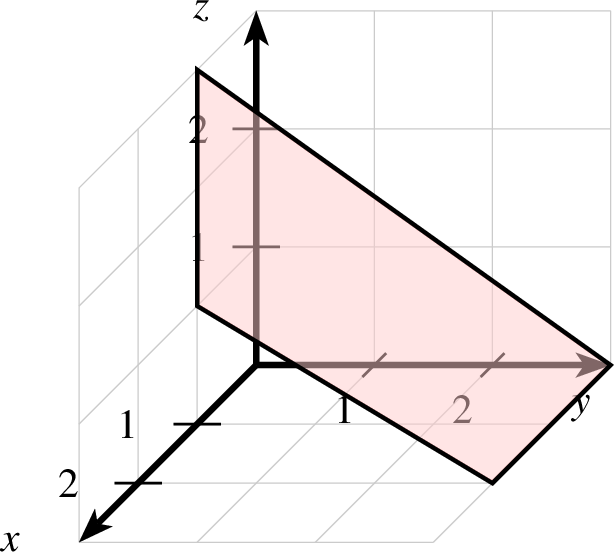
| kreis-3d-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 pstricks 2 koordinatensystem x=-3,3 y=-3,3 z=-2,2 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 3 kreis farbe=black,solid,red!20 linie=1,solid,red parameter="opacity=0.5" p=0,0,0 r=1,-2.25,1 4 kreis p=2,0,0 r=1,-1,0.75 r=0,180 |
8.2.4 Kurven zeichnen
Ähnlich zum Linienbefehl gibt es noch den Befehl der Kurve ebenfalls im
dreidimensionalen Raum. Hier wird der Befehl kurve einfach um die
 -Koordinate erweitert.
-Koordinate erweitert.
kurve
[layer=< 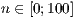 >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt ( 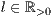 )>,<Linienart>[,"<Pfeiltyp>"]]
)>,<Linienart>[,"<Pfeiltyp>"]]
[parameter="<Pstricksbefehle>"]
< 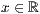 >,<
>,< 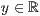 >,<
>,< 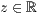 > beliebig oft
> beliebig oft
ende
Dabei ist zu beachten, dass bei diesem Befehl die Kurve durch alle
angegebenen Punkte geht.
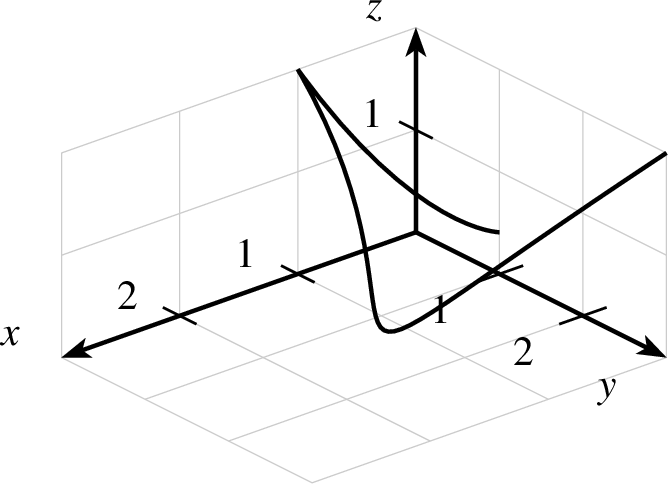
| kurve-3d-ptxt.ptxt |
|---|
| 1 einstellung coortype=0 2 achsen 3 gitter 4 kurve farbe=black linie=1,solid 5 0,0,0 6 1,0,2 7 1,2,0 8 3,2,0 9 0,3,2 10 ende |
 -Koordinate erweitert. Dabei werden intern die
Punkte in zweidimensionale Punkte übertragen und dann weiter verarbeitet.
-Koordinate erweitert. Dabei werden intern die
Punkte in zweidimensionale Punkte übertragen und dann weiter verarbeitet.bezier
[layer=<
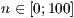 >]
>][farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (
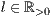 )>,<Linienart>[,"<Pfeiltyp>"]]
)>,<Linienart>[,"<Pfeiltyp>"]][parameter="<Pstricksbefehle>"]
<
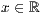 >,<
>,< 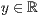 >,<
>,< 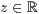 > beliebig oft
> beliebig oftende
| bezier-3d-ptxt.ptxt |
|---|
| 1 einstellung coortype=0 pstricks 2 achsen 3 gitter 4 bezier farbe=black linie=1,solid 5 0,0,0 6 1,0,2 7 1,2,0 8 3,2,0 9 0,3,2 10 ende |
8.2.5 Beschriftungen, Punkte und Kreuze im 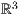 zeichnen
zeichnen
Beschriftungen
Auch im 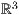 gibt es denn Befehl der Beschriftung, der wie folgt aussieht:
gibt es denn Befehl der Beschriftung, der wie folgt aussieht:
beschriftung
[layer=< 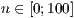 >]
>]
[farbe=<Linienfarbe>]
p=< 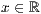 >,<
>,< 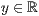 >,<
>,< 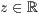 >
>
text="<Text>",<Textwinkel in Grad>,<Drehung in Grad>
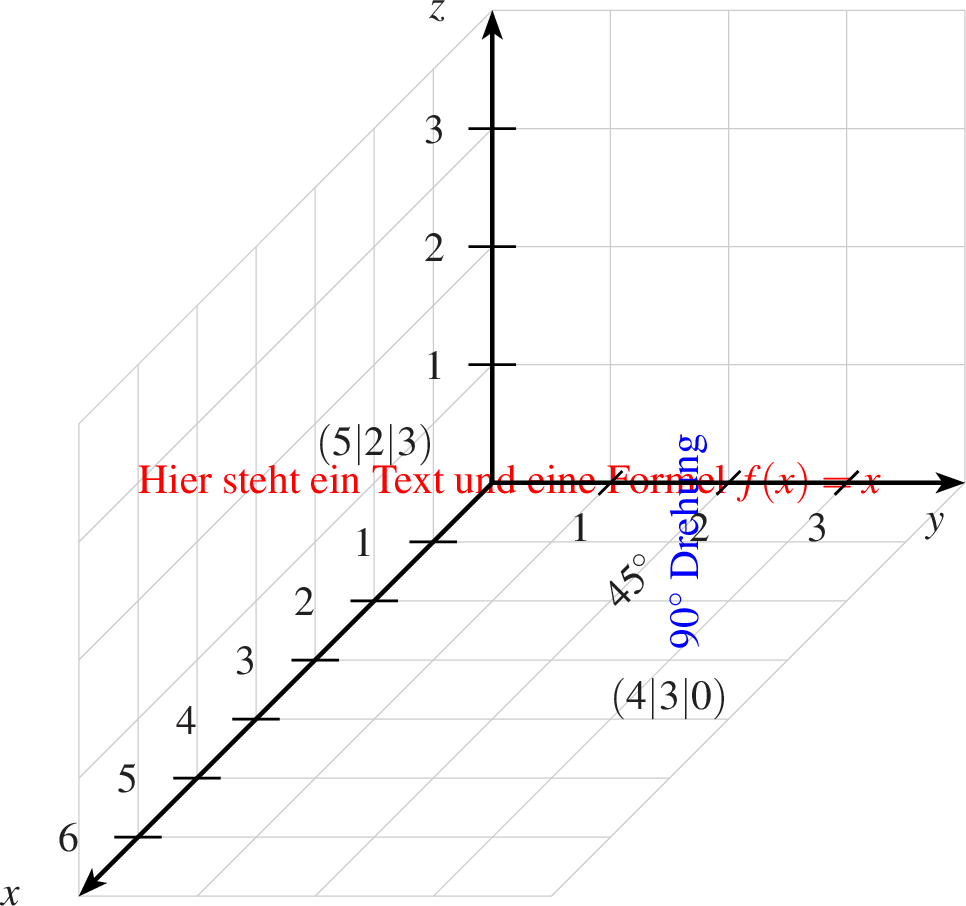
| beschriftung-3d-ptxt.ptxt |
|---|
| 1 grenzengitter x=0,7 y=0,4 z=0,4 2 achsen 3 beschriftung farbe=red p=6,0,3 text="Hier steht ein Text und eine Formel $f(x)=x$",0,r 4 5 beschriftung farbe=blue p=1,2,0 text="$90^{\circ}$ Drehung",90,0 6 beschriftung p=4,3,1 text="$45^{\circ}$",45,45 7 beschriftung p=4,3,0 text="$(4|3|0)$",0,45 8 beschriftung p=5,2,3 text="$(5|2|3)$",0,225 |
Punkte zeichnen
Möchte man einen Koordinatenpunkt 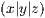 mit Beschriftung versehen, so gibt
es den Befehl punkt, an den man einen Text übergeben kann. Die
Syntax sieht wie folgt aus:
mit Beschriftung versehen, so gibt
es den Befehl punkt, an den man einen Text übergeben kann. Die
Syntax sieht wie folgt aus:
punkt
[layer=< 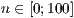 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 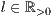 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 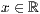 >,<
>,< 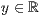 >,<
>,< 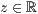 >
>
r=<Radius 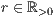 des Punktes>
des Punktes>
[text="<Text>"[,<Drehung in Grad>]]
Der Radius eines Punktes ist standardmäßig auf 0,05 gesetzt.
| punkt-3d-ptxt.ptxt |
|---|
| 1 einstellung alpha=45 beta=30 coortype=2 pstricks 2 grenzengitter x=0,6 y=0,4 z=0,2 3 achsen 4 punkt farbe=black,solid,red!20 linie=1,solid parameter="opacity=0.5" p=0,0,0 r=1 text="Hallo Anna Lena",-30 5 punkt p=5,2,0 text="$(5|2|0)$" 6 punkt p=3,1,0 r=0.1 |
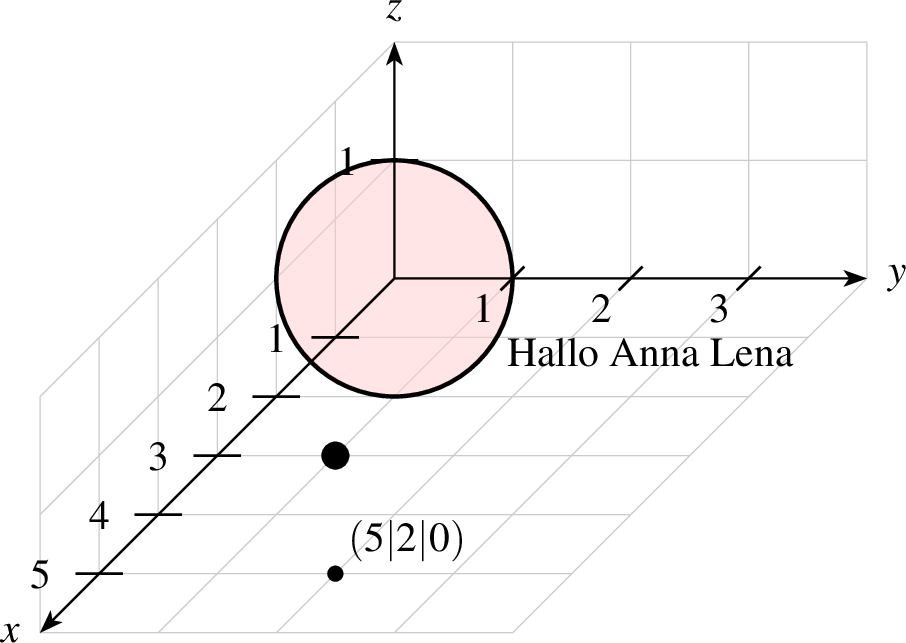
Kreuze zeichnen
Möchte man anstelle eines Koordinatenpunkt 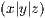 ein Kreuz zeichnen,
so gibt es den Befehl kreuz, an den man einen Text übergeben
kann. Die Syntax sieht wie folgt aus:
ein Kreuz zeichnen,
so gibt es den Befehl kreuz, an den man einen Text übergeben
kann. Die Syntax sieht wie folgt aus:
kreuz
[layer=< 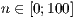 >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt ( 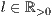 )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
p=< 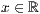 >,<
>,< 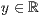 >,<
>,< 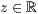 >
>
r=<Länge des Kreuzes 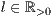 >[,<Drehwinkel des Kreuzes in Grad>]
>[,<Drehwinkel des Kreuzes in Grad>]
[text="<Text>"[,<Drehung in Grad>]]
Standardmäßig ist die Länge des Kreuzes auf 0,5 LE gesetzt und der Drehwinkel
beträgt 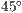 . Die Drehung des Textes ist als Standard ebenfalls
. Die Drehung des Textes ist als Standard ebenfalls 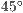 .
.
| kreuz-3d-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 2 grenzengitter x=0,6 y=0,4 z=0,2 3 achsen 4 kreuz farbe=black linie=1,solid parameter="" p=1,1,0 r=1,30 text="Hallo Anna Lena",-30 5 kreuz p=5,2,0 text="$(5|2|0)$" 6 kreuz linie=2,solid p=3,1,0 r=1,0 7 r |
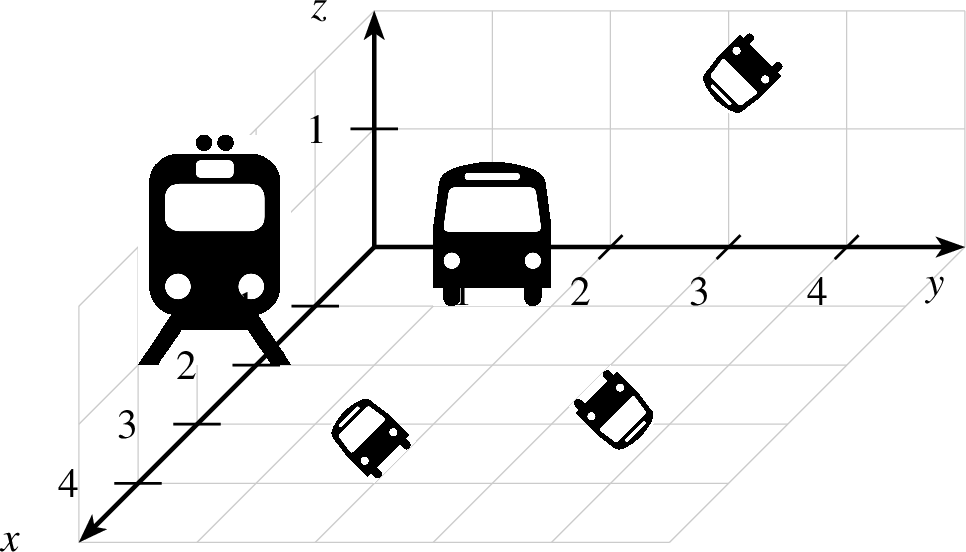
8.2.6 Grafiken einfügen
Möchte man eine Grafik in eine Zeichung mit einfügen, so gibt es wie
unter 4.5 beschrieben den Befehl bild, der einem dies
ermöglicht. Dieser ist ebenfalls für dreidimensionale Objekte erweitert.
bild
[layer=< 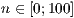 >]
>]
p=< 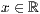 >,<
>,< 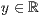 >,<
>,< 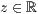 >
>
r=<Breite des Bildes 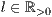 >[,<Drehwinkel des Bildes in Grad>]
>[,<Drehwinkel des Bildes in Grad>]
<"Dateiname">
| bild-3d-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 2 grenzengitter x=0,5 y=0,5 z=0,2 3 achsen 4 bild p=1,1,0 r=1 Abbildungen/bus.eps 5 bild p=4,2,0 r=0.5,45 Abbildungen/bus.eps 6 bild p=1,4,2 r=0.5,135 Abbildungen/bus.eps 7 bild p=2,3,0 r=0.5,225 Abbildungen/bus.eps 8 bild p=4,0,1 r=1.3 Abbildungen/zug.eps 9 |
8.3 Koordinatensysteme und Gitter im 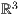
8.3.1 Einfache Koordinatensysteme
Die Syntax für ein dreidimensionales koordinatensystem ist:
koordinatensystem
[layer=<  >]
>]
x=< 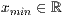 >,<
>,< 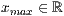 > y=<
> y=< 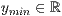 >,<
>,< 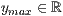 > z=<
> z=< 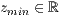 >,<
>,< 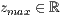 >
>
einteilung=< 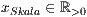 >,<
>,< 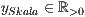 >,<
>,< 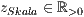 >
>
[linie=<Linienstärke in pt ( 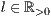 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
skala=<keine|nurstriche|nureins|normal|strichundeins>
text="Text an der 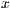 -Achse","Text an der
-Achse","Text an der 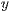 -Achse","Text an der
-Achse","Text an der  -Achse"
-Achse"
Einige Beispiele
Hier nun ein paar einfache Beispiele für Koordinatenachsen:
| koordinatensystem-3d-ptxt.ptxt |
|---|
| 1 koordinatensystem x=-4,4 y=-3,3 z=-2,2 einteilung=2,1,0.5 linie=2,solid,black skala=normal text="$x$","$y$","$z$" |
| koordinatensystem-3d-2-ptxt.ptxt |
|---|
| 1 koordinatensystem x=-4,4 y=-2,2 z=-2,2 einteilung=2,1,0.5 linie=2,solid,black,"-" skala=normal text="$x$","$y$","$z$" |
8.3.2 Gitter zeichnen im 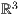
Die Syntax für ein Gitter im 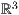 lautet
lautet
kariert
[layer=< 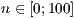 >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt ( 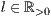 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
dx=< 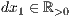 >,<
>,< 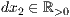 >,<
>,< 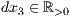 >
>
dy=< 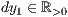 >,<
>,< 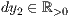 >,<
>,< 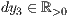 >
>
dz=< 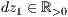 >,<
>,< 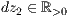 >,<
>,< 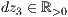 >
>
x=< 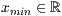 >,<
>,< 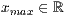 >
>
y=< 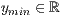 >,<
>,< 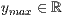 >
>
z=< 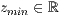 >,<
>,< 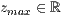 >
>
| kariert-3d-ptxt.ptxt |
|---|
| 1 achsen 2 kariert farbe=lightgray linie=1,solid dx=0.5,0,0 dy=1,0,0 dz=0.5,0,0 x=-0,3 y=0,3 z=0,3 |
8.4 Plotten von Funktionen und Daten im 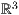
Analog zu Abschnitt 6 gibt es auch für den 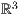 die
Möglichkeit Funktionen zu zeichnen.
die
Möglichkeit Funktionen zu zeichnen.
8.4.1 Funktionen zeichnen im 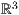
Um Funktionen der Form 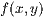 zu zeichnen habe ich den Befehl
graph erweitert. Die Syntax ist die folgende:
zu zeichnen habe ich den Befehl
graph erweitert. Die Syntax ist die folgende:
graph
[layer=< 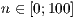 >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt ( 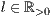 )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=< 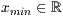 >,<
>,< 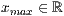 >
>
y=< 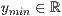 >,<
>,< 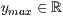 >
>
[z=< 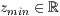 >,<
>,< 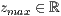 >]
>]
<Funktionsterm 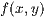 >
>
Hierbei wird der Funktionsterm mit den Variablen 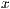 und
und 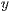 in der
algebraischen Notation erwartet. Werden
in der
algebraischen Notation erwartet. Werden 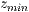 und
und 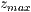 nicht
angegeben, so wird die Funktion nicht ohne Beschränkung gezeichnet. Werden
diese Werte angegeben, so werden intern die Werte
nicht
angegeben, so wird die Funktion nicht ohne Beschränkung gezeichnet. Werden
diese Werte angegeben, so werden intern die Werte 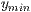 und
und 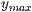 beschränkt.
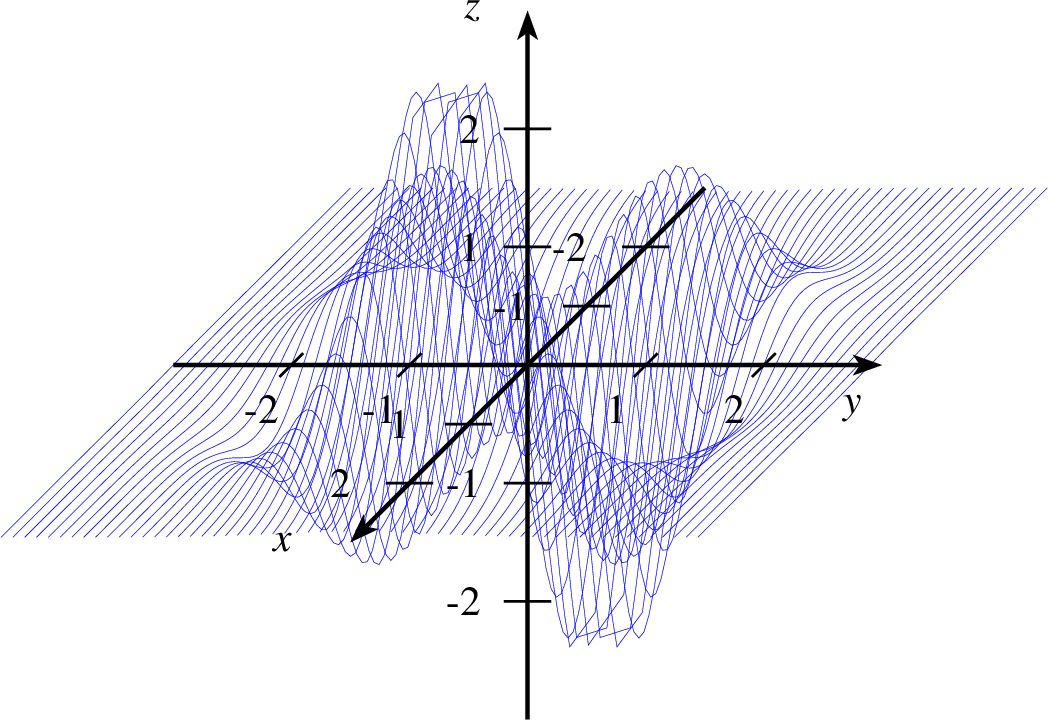
Im Folgenden betrachte ich einmal die Funktion
beschränkt.
Im Folgenden betrachte ich einmal die Funktion
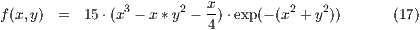
genauer.
Es sind dabei die gleichen Parameter wie in PSTricks
implementiert2. Es gibt dabei die
folgenden Parameter.
| Name | Vorgabe |
| xPlotpoints | 25 |
| yPlotpoints | 25 |
| drawStyle | xLines |
| graph-3d-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 2 achsen 3 graph layer=50 farbe=blue linie=0.1,solid parameter="xPlotpoints=70,yPlotpoints=60" x=-3,3 y=-3,3 z=-3,3 10*(x^3-x*y^2-x/4)*exp(-(x^2+y^2)) |
| graph-3d-2-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 pstricks 2 achsen 3 graph layer=50 farbe=blue linie=0.1,solid parameter="xPlotpoints=70,yPlotpoints=60,hiddenLine=true" x=-3,3 y=-3,3 10*(x^3-x*y^2-x/4)*exp(-(x^2+y^2)) |
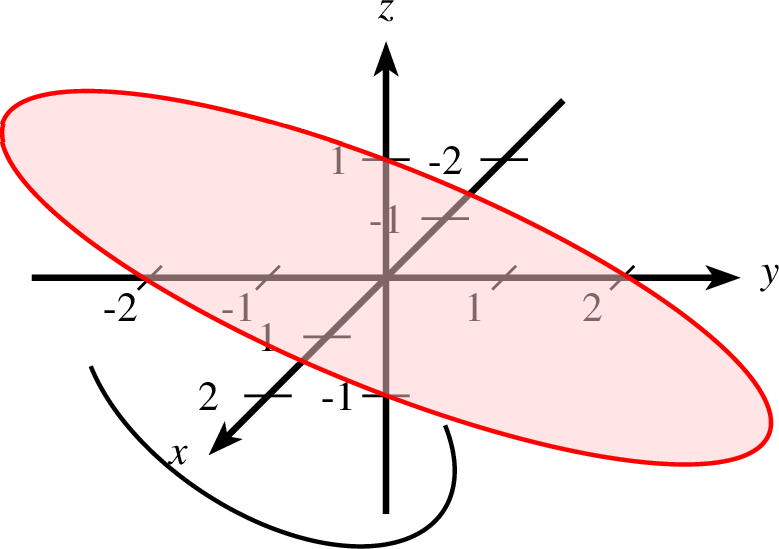
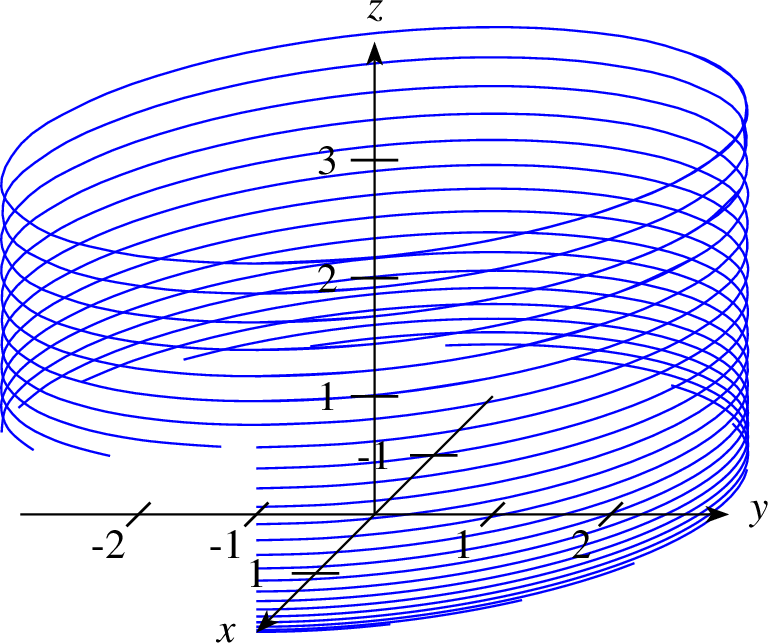
8.4.2 Parametrisierte Kurven im 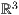
Im 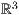 kann ebenfalls eine Parametrisierung einer Kurve dargestellt werden.
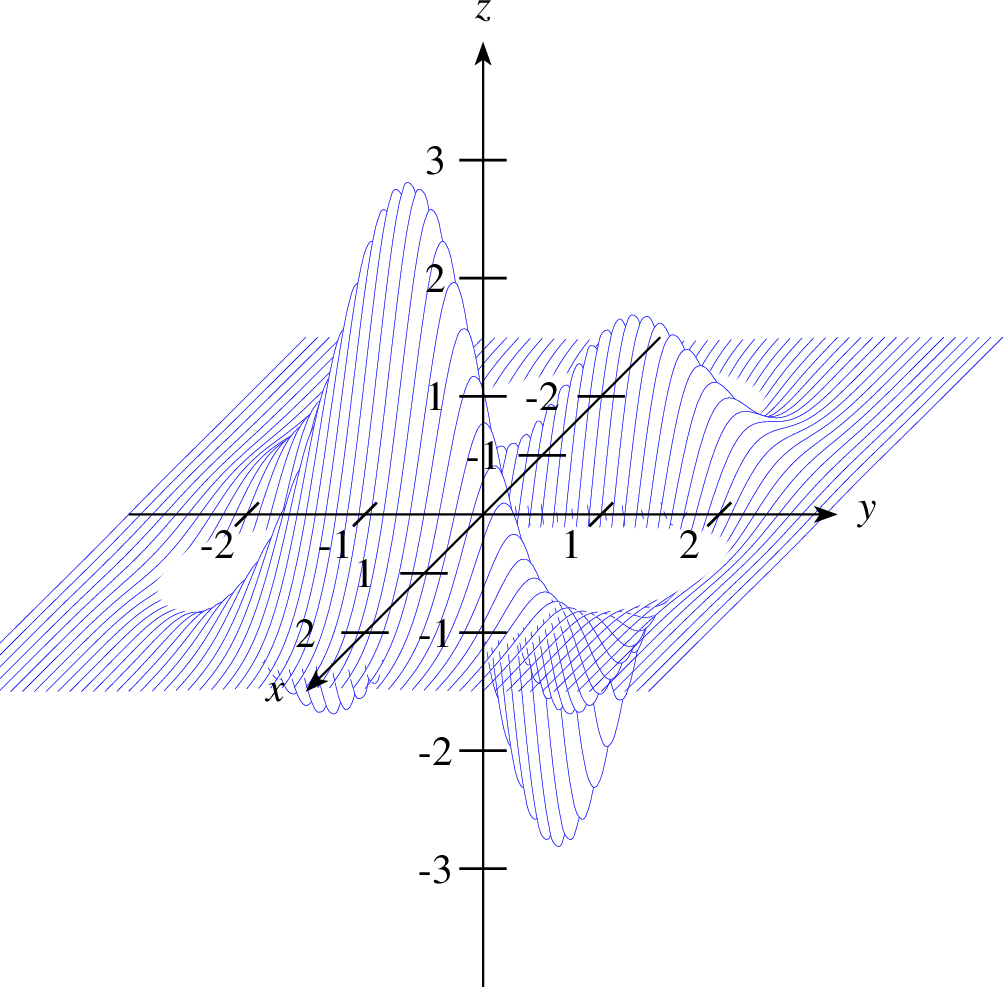
Ein Beispiel hierfür ist die Darstellung einer Spirale in der Form
kann ebenfalls eine Parametrisierung einer Kurve dargestellt werden.
Ein Beispiel hierfür ist die Darstellung einer Spirale in der Form
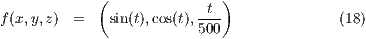
Die Syntax des Befehls ist die folgende:
parametricplot
[layer=< 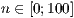 >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt ( 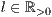 )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
t=< 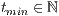 >,<
>,< 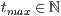 >
>
[u=< 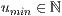 >,<
>,< 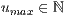 >]
>]
<Funktionsterm 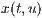 >,<Funktionsterm
>,<Funktionsterm 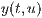 >,<Funktionsterm
>,<Funktionsterm 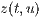 >
>
Wobei 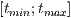 und
und 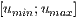 die jeweiligen Definitionsintervalle beschreiben.
die jeweiligen Definitionsintervalle beschreiben.
| parametricplot-3d-ptxt.ptxt |
|---|
| 1 einstellung coortype=1 pstricks 2 achsen 3 parametricplot layer=50 farbe=blue linie=1,solid parameter="plotstyle=curve" t=0,1000 cos(t),sin(t),t/500 |
| parametricplot-3d-2-ptxt.ptxt |
|---|
| 1 achsen 2 parametricplot layer=50 farbe=blue linie=0.5,solid parameter="plotstyle=curve" t=0,100 u=0,5 2*cos(t)*u,3*sin(t)*u,(u^2)/8 |
8.4.3 Plotten von Daten im 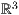
Das Plotten von Daten im dreidimensionalen Raum läuft effektiv analog zum
zweidimensionalen Raum ab. Siehe dazu Abschnitt 6.10. Es wird
jeweils nur die  -Koordinate ergänzt. Die Syntax ist dabei bei
allen Funktionen die folgende:
-Koordinate ergänzt. Die Syntax ist dabei bei
allen Funktionen die folgende:
[<fileplot|listplot|dataplot>]
[layer=< 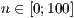 >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt ( 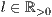 )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
[lese <Dateiname>] oder < 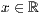 >,<
>,< 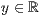 >,<
>,< 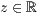 > beliebig oft
> beliebig oft
ende
| listplot-3d-ptxt.ptxt |
|---|
| 1 achsen 2 listplot farbe=red linie=1,solid parameter="plotstyle=curve" 3 0,0,0 4 1,0,1 5 2,0.2,0.7 6 0,0.3,0.7 7 1,2,2 8 1,1,0 9 3,4,1 10 2,2,2 11 ende |
8.5 Objekte für die analytische Geometrie
Für meinen Mathematikunterricht in der Oberstufe brauche ich Elemente wie Geraden, Ebenen und Kugeln. Um dies einfach eingeben zu können, habe ich mir ein paar Zeichenelemente definiert.
8.5.1 Geraden im Raum
Die vektorielle Parametergleichung einer Geraden ist gegeben mit

wobei 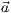 der Stützvektor und
der Stützvektor und 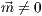 der Richtungsvektor
der Geraden
der Richtungsvektor
der Geraden 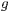 sind.
Die Syntax ist dabei ähnlich zur Linie:
sind.
Die Syntax ist dabei ähnlich zur Linie:
gerade
[layer=< 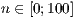 >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt ( 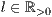 )>,<Linienart>[,"<Pfeiltyp>"]]
)>,<Linienart>[,"<Pfeiltyp>"]]
[parameter="<Pstricksbefehle>"]
p=< 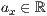 >,<
>,< 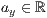 >,<
>,< 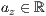 >
>
p=< 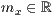 >,<
>,< 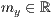 >,<
>,< 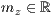 >
>
r=< 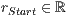 >,<
>,< 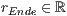 >
>
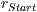 und
und 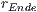 sind dabei die Werte, für die der Start- und
Endpunkt berechnet werden.
sind dabei die Werte, für die der Start- und
Endpunkt berechnet werden.
| gerade-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 2 achsen 3 gitter 4 gerade farbe=red linie=1,solid,"->" p=1,1,2 p=1,2,0 r=-0.25,2 5 punkt p=1,1,2 r=0.04 6 punkt p=2,3,2 r=0.04 |
8.5.2 Ebenengleichungen
Neben der Geraden ist die Ebene ein wichtiges Objekt in der analytischen Geometrie. Dabei gibt es verschiedene Darstellungsformen einer Ebene. Ich habe in meinem Skript die Parametergleichung und Koordinatengleichung realisiert. Die anderen formen sind jeweils einfach umwandelbar.
Parametergleichung einer Ebene
Die vektorielle Parametergleichung einer Ebene ist gegeben mit
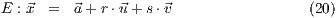
wobei 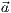 der Stützvektor und
der Stützvektor und 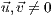 die
Richtungsvektoren und
die
Richtungsvektoren und 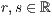 die Ebenenparameter sind.
Die Syntax ist dabei die Folgende:
die Ebenenparameter sind.
Die Syntax ist dabei die Folgende:
ebene
[layer=< 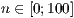 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 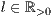 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 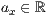 >,<
>,< 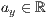 >,<
>,< 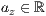 >
>
p=< 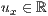 >,<
>,< 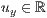 >,<
>,< 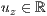 >
>
p=< 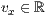 >,<
>,< 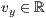 >,<
>,< 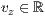 >
>
[r=< 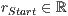 >,<
>,< 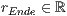 >]
>]
[r=< 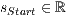 >,<
>,< 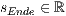 >]
>]
Sind die Ebenenparameter nicht gesetzt, so ist der Startwert 0 und der Endwert
1.
| ebene-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 pstricks 2 achsen 3 gitter 4 ebene linie=1,solid p=2,0,2 p=1,2,0 p=-1,3,1 |
Die Koordinatengleichung einer Ebene
Eine Ebene im dreidimensionalen Anschauungsraum lässt sich stets durch eine
lineare Gleichung der Form

darstellen, die man als Koordinatengleichung bezeichnet.
Die Syntax ist dabei die Folgende:
ebene
[layer=< 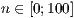 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 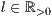 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
r=< 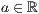 >,<
>,< 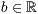 >,<
>,< 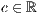 >,<
>,< 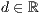 >[,<
>[,< 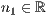 >][,<
>][,< 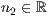 >]
>]
Wobei 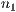 und
und 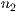 standardmäßig auf 1 gesetzt sind. Diese Werte stehen
dafür, wie weit eine Ebene gezeichnet werden soll.
standardmäßig auf 1 gesetzt sind. Diese Werte stehen
dafür, wie weit eine Ebene gezeichnet werden soll.
Beispiele
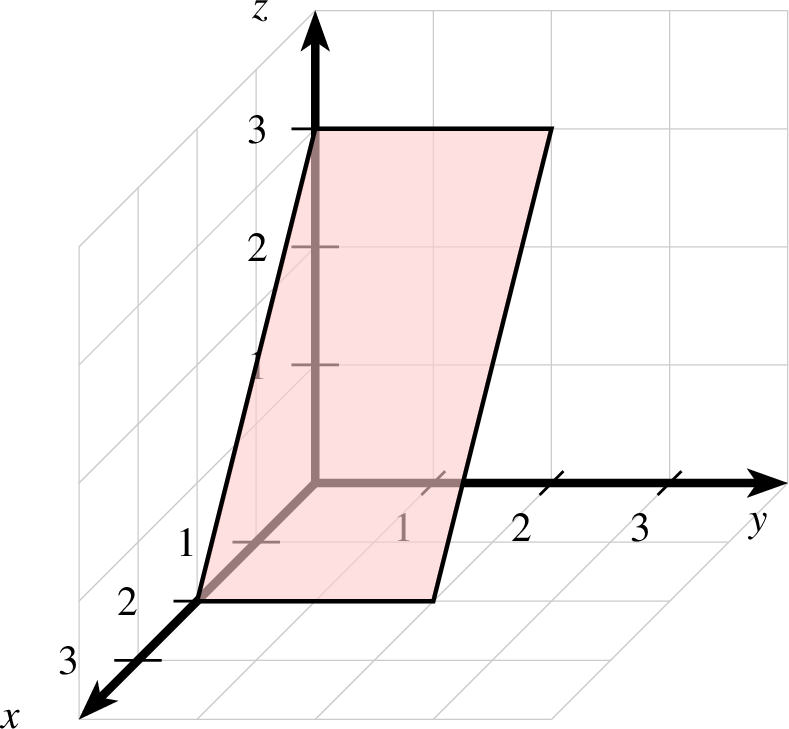
Im Folgenden sind drei Ebenen in der Koordinatenform dargestellt.
| ebene-2-ptxt.ptxt |
|---|
| 1 gitter 2 koordinatensystem x=0,4 y=0,4 z=0,4 einteilung=1,1,1 linie=2,solid,black skala=normal text="$x$","$y$","$z$" 3 ebene layer=11 farbe=black,shape,red!20 linie=1,solid r=6,6,4,12 4 |
| ebene-3-ptxt.ptxt |
|---|
| 1 gitter 2 koordinatensystem x=0,4 y=0,4 z=0,4 einteilung=1,1,1 linie=2,solid,black skala=normal text="$x$","$y$","$z$" 3 ebene layer=11 farbe=black,shape,red!20 linie=1,solid r=6,0,4,12,2 4 |
| ebene-4-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 2 gitter 3 koordinatensystem x=0,3 y=0,3 z=0,3 einteilung=1,1,1 linie=2,solid,black skala=normal text="$x$","$y$","$z$" 4 ebene layer=11 farbe=black,shape,red!20 linie=1,solid r=6,0,0,12,2,3 5 |
Die Normalengleichung einer Ebene
Die Normalengleichung einer Ebene hat die Form

oder

wobei 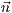 ein Normalenvektor der Ebene,
ein Normalenvektor der Ebene, 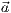 der Ortsvektor eines
beliebigen Punktes ist, der in der Ebene liegt und
der Ortsvektor eines
beliebigen Punktes ist, der in der Ebene liegt und 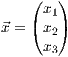 der Vektor der Unbekannten
ist.
Die Syntax ist dabei die Folgende:
der Vektor der Unbekannten
ist.
Die Syntax ist dabei die Folgende:
ebene
[layer=< 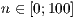 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 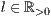 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 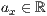 >,<
>,< 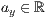 >,<
>,< 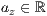 >
>
p=< 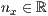 >,<
>,< 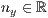 >,<
>,< 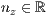 >
>
[r=< 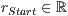 >,<
>,< 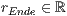 >]
>]
[r=< 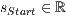 >,<
>,< 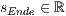 >]
>]
Wobei 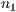 und
und 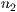 standardmäßig auf 1 gesetzt sind. Diese Werte stehen
dafür, wie weit eine Ebene gezeichnet werden soll.
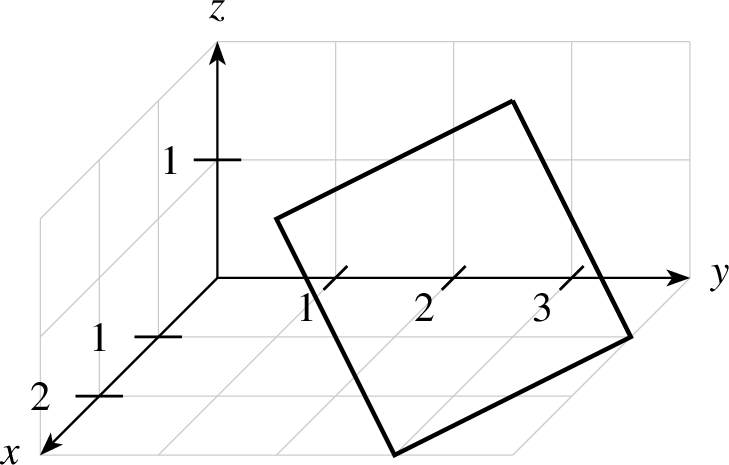
In der Abbildung 8.5.2 ist die Ebene
standardmäßig auf 1 gesetzt sind. Diese Werte stehen
dafür, wie weit eine Ebene gezeichnet werden soll.
In der Abbildung 8.5.2 ist die Ebene 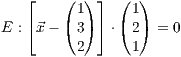 dargestellt.
dargestellt.
| ebene-5-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 pstricks 2 achsen 3 gitter 4 ebene linie=1,solid p=1,3,2 p=1,2,1 |
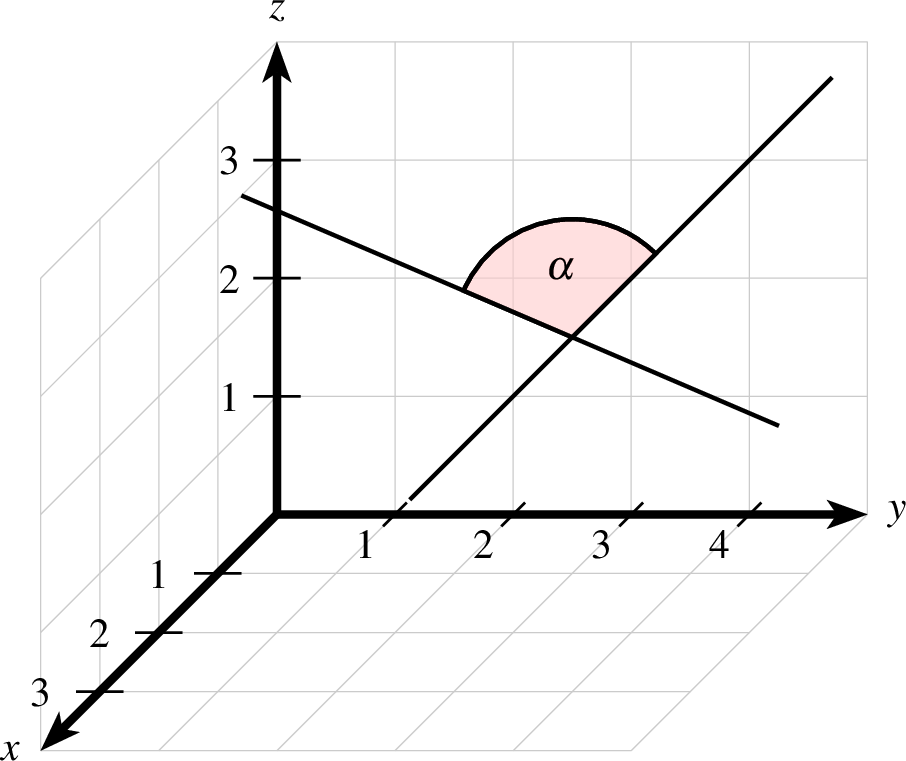
8.5.3 Winkel im 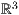
Analog zum Abschnitt 4.6.1 gibt es auch im dreidimensionalen
Winkelmarkierungen. Die Syntax ist dann:
winkel
[layer=< 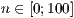 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 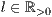 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 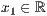 >,<
>,< 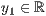 >,<
>,< 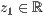 >
>
p=< 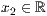 >,<
>,< 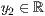 >,<
>,< 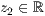 >
>
p=< 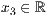 >,<
>,< 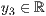 >,<
>,< 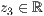 >
>
r=<Radius 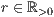 des Bogens>,<a|i>
des Bogens>,<a|i>
text="<Text>"
| winkel-3d-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 pstricks 2 gitter 3 koordinatensystem x=0,4 y=0,5 z=0,4 einteilung=1,1,1 linie=2,solid,black skala=normal text="$x$","$y$","$z$" 4 gerade p=-2,7,6 p=-3,4,4 r=-1.25,-0.6 5 gerade p=1,-4,5 p=0,-7,3 r=-1.25,-0.6 6 winkel farbe=black,shape,red!20 linie=1,solid p=-2,7,6 p=1,3,2 p=1,-4,5 r=1,i text="$\alpha$" |
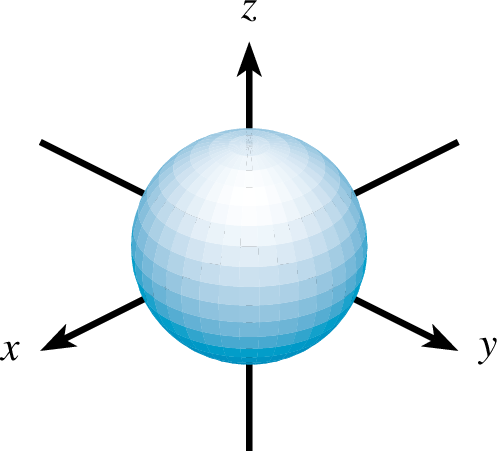
8.5.4 Kugeln
Eine Kugel wird einfach mit dem Befehl kugel erstellt, wobei
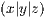 der Mittelpunkt der Kugel ist.
der Mittelpunkt der Kugel ist.
kugel
[layer=< 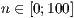 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 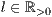 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 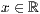 >,<
>,< 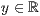 >,<
>,< 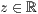 >
>
r=< 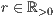 >
>
| kugel-ptxt.ptxt |
|---|
| 1 einstellung coortype=0 pstricks 2 koordinatensystem x=-2.5,2.5 y=-2.5,2.5 z=-2,2 einteilung=1,1,1 skala=keine text="$x$","$y$","$z$" 3 kugel farbe=blue,shape,blue!20 linie=1,solid parameter="SegmentColor={[cmyk]{0.8,0.2,0.11,0}}" p=0,0,0 r=1 |
8.6 Körper im 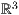
Neben der Kugel gibt es auch noch weitere Körper im dreidimensionalen Raum zu zeichnen. Dazu gehören die folgenden Objekte:
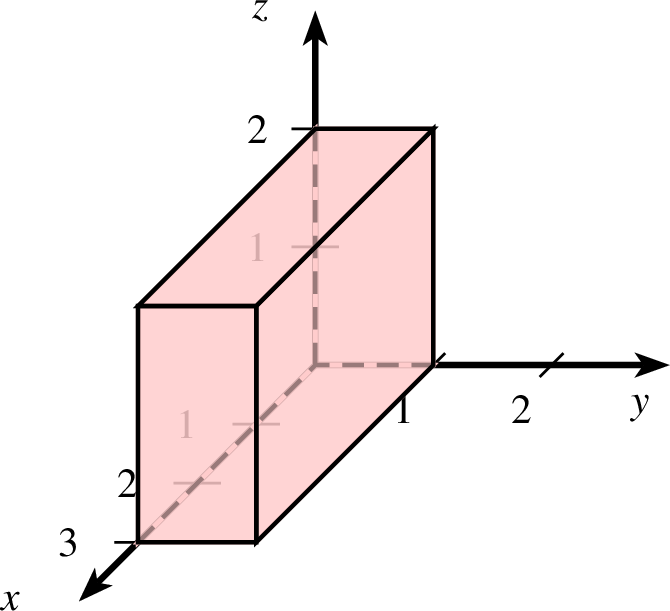
8.6.1 Ein Quader
Ein Quader ist definiert über einen Eckpunkt 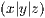 und seine
Länge, Breite und Höhe definiert. Die Syntax ist dabei die folgende:
und seine
Länge, Breite und Höhe definiert. Die Syntax ist dabei die folgende:
quader
[layer=< 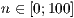 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 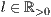 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 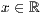 >,<
>,< 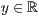 >,<
>,< 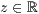 >
>
r=< 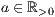 >,<
>,< 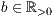 >,<
>,< 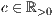 >
>
| quader-ptxt.ptxt |
|---|
| 1 koordinatensystem x=0,4 y=0,3 z=0,3 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 2 quader farbe=black,shape,red!20 linie=1,solid parameter="" p=0,0,0 r=3,1,2 |
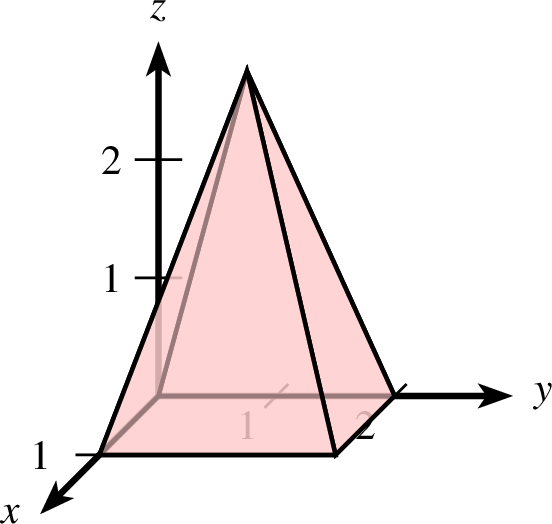
8.6.2 Eine Pyramide und ein Pyramidenstumpf
Eine Pyramide ist definiert über einen Eckpunkt 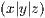 und seine
Länge, Breite und Höhe definiert. Die Syntax ist dabei die folgende:
und seine
Länge, Breite und Höhe definiert. Die Syntax ist dabei die folgende:
pyramide
[layer=< 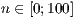 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 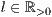 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 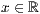 >,<
>,< 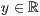 >,<
>,< 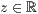 >
>
r=< 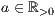 >,<
>,< 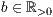 >,<
>,< 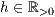 >
>
| pyramide-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 pstricks 2 koordinatensystem x=0,2 y=0,3 z=0,3 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 3 pyramide farbe=black,shape,red!20 linie=1,solid p=1,0,0 r=1,2,3 |
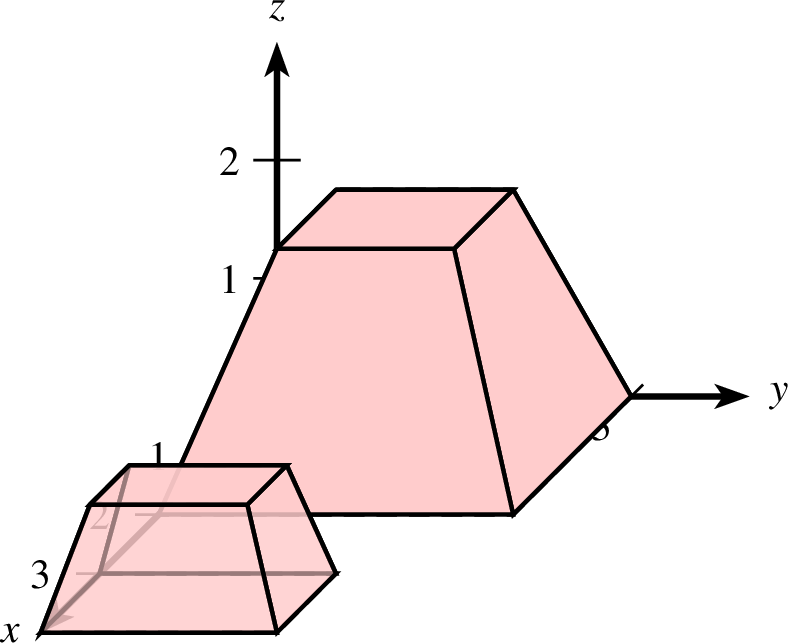
pyramidestumpf
[layer=<
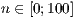 >]
>][farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (
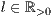 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]][parameter="<Pstricksbefehle>"]
p=<
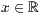 >,<
>,< 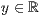 >,<
>,< 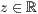 >
>r=<
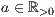 >,<
>,< 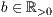 >,<
>,< 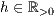 >,<
>,< 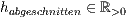 >
>
| pyramidestumpf-ptxt.ptxt |
|---|
| 1 einstellung coortype=2 pstricks 2 koordinatensystem x=0,4 y=0,4 z=0,3 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 3 pyramidestumpf farbe=black,solid,red!20 linie=1,solid p=2,0,0 r=2,3,4,2 4 pyramidestumpf farbe=black,shape,red!20 linie=1,solid p=4,0,0 r=1,2,3,1 |
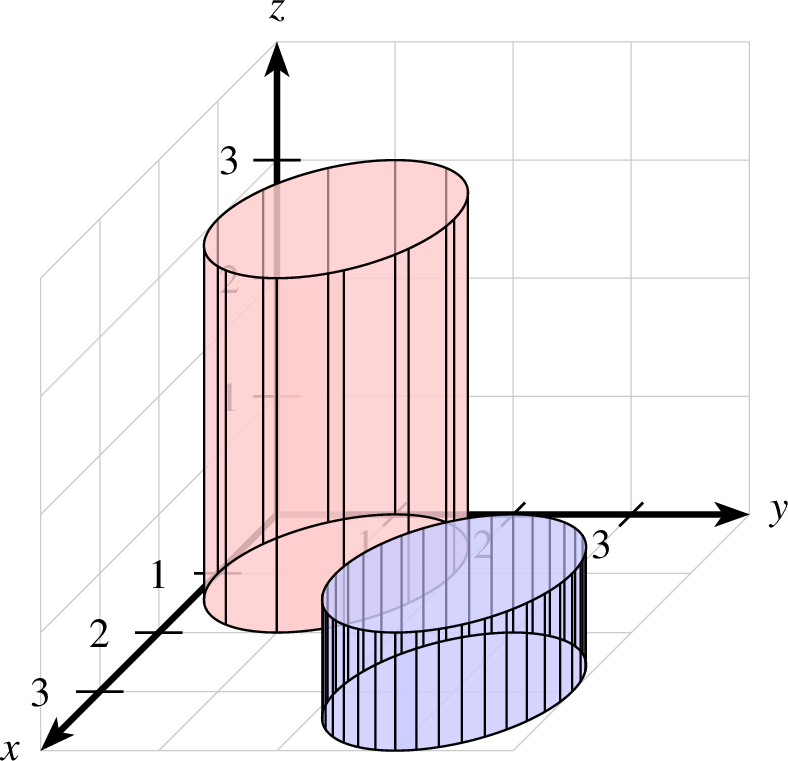
8.6.3 Ein Kreiszylinder
Ein Kreiszylinder ist definiert über seinen Mittelpunkt 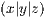 ,
seinen Radius und seine Höhe.
Die Syntax ist dabei die folgende:
,
seinen Radius und seine Höhe.
Die Syntax ist dabei die folgende:
zylinder
[layer=< 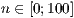 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 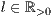 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 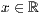 >,<
>,< 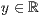 >,<
>,< 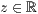 >
>
r=< 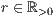 >,<
>,< 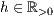 >[,<
>[,< 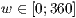 >]
>]
Dabei gibt 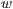 an, in welchen Abständen die Seitenlinien gezeichnet
werden. Der Standardwert ist dabei 30.
an, in welchen Abständen die Seitenlinien gezeichnet
werden. Der Standardwert ist dabei 30.
| zylinder-ptxt.ptxt |
|---|
| 1 einstellung pstricks 2 gitter 3 koordinatensystem x=0,4 y=0,4 z=0,4 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 4 zylinder farbe=black,shape,red!20 linie=0.5,solid p=1,1,0 r=1,3 5 zylinder farbe=black,shape,blue!20 linie=0.5,solid p=3,3,0 r=1,1,10 |
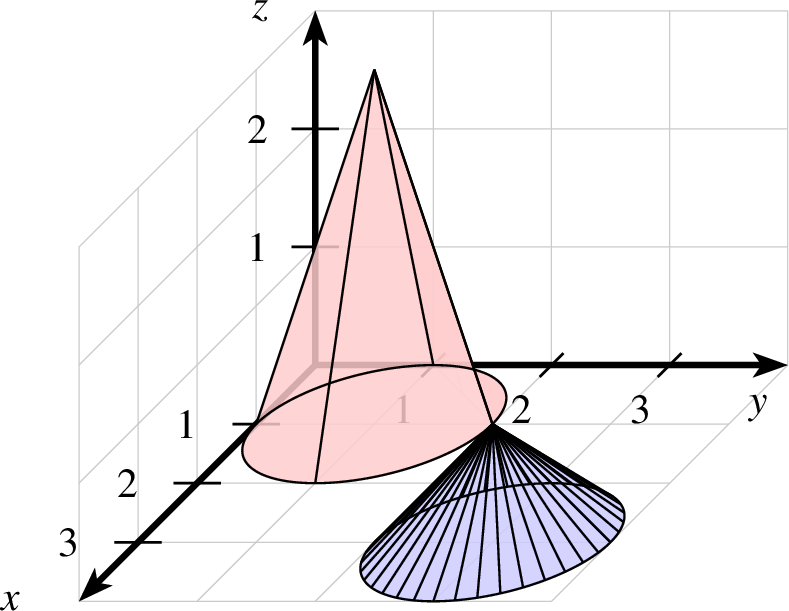
8.6.4 Ein Kegel und ein Kegelstumpf
Ein Kegel ist definiert über seinen Mittelpunkt 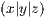 , seinen Radius und
seine Höhe. Die Syntax ist die folgende:
, seinen Radius und
seine Höhe. Die Syntax ist die folgende:
kegel
[layer=< 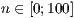 >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt ( 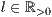 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]]
[parameter="<Pstricksbefehle>"]
p=< 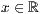 >,<
>,< 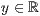 >,<
>,< 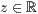 >
>
r=< 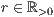 >,<
>,< 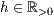 >[,<
>[,< 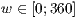 >]
>]
Dabei gibt 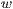 an, in welchen Abständen die Seitenlinien gezeichnet
werden. Der Standardwert ist dabei 30.
an, in welchen Abständen die Seitenlinien gezeichnet
werden. Der Standardwert ist dabei 30.
| kegel-ptxt.ptxt |
|---|
| 1 gitter 2 koordinatensystem x=0,4 y=0,4 z=0,3 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 3 kegel farbe=black,shape,red!20 linie=0.5,solid p=1,1,0 r=1,3 4 kegel farbe=black,shape,blue!20 linie=0.5,solid p=3,3,0 r=1,1,10 |
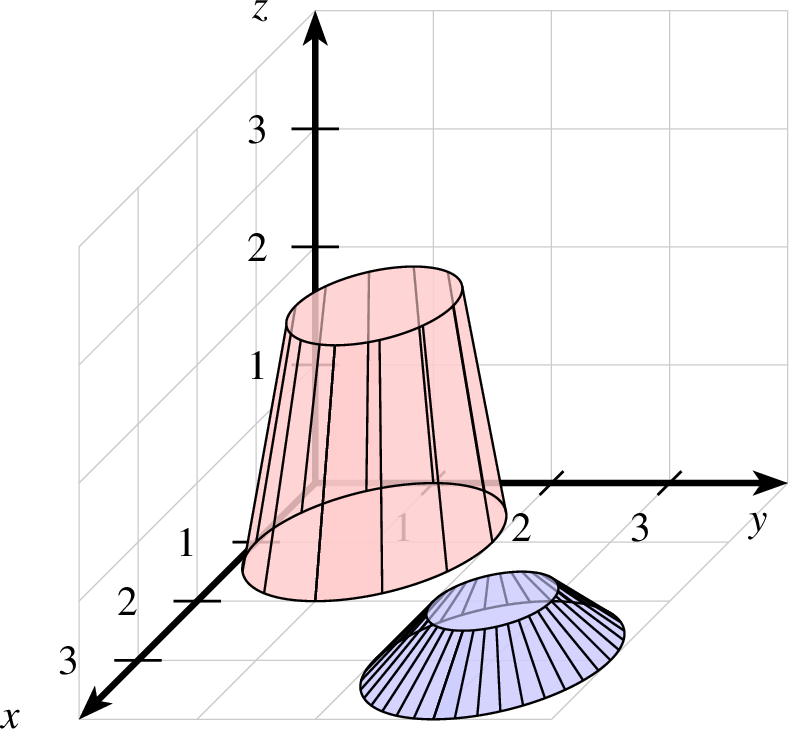
kegelstumpf
[layer=<
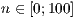 >]
>][farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (
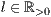 )>,<Linienart>[,<Linienfarbe>]]
)>,<Linienart>[,<Linienfarbe>]][parameter="<Pstricksbefehle>"]
p=<
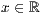 >,<
>,< 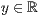 >,<
>,< 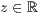 >
>r=<
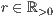 >,<
>,< 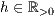 >,<
>,< 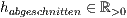 >[,<
>[,< 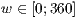 >]
>]
| kegelstumpf-ptxt.ptxt |
|---|
| 1 gitter 2 koordinatensystem x=0,4 y=0,4 z=0,4 einteilung=1,1,1 skala=normal text="$x$","$y$","$z$" 3 kegelstumpf farbe=black,shape,red!20 linie=0.5,solid p=1,1,0 r=1,3,1 4 kegelstumpf farbe=black,shape,blue!20 linie=0.5,solid p=3,3,0 r=1,1,0.5,10 |



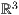
 mit Text
mit Text 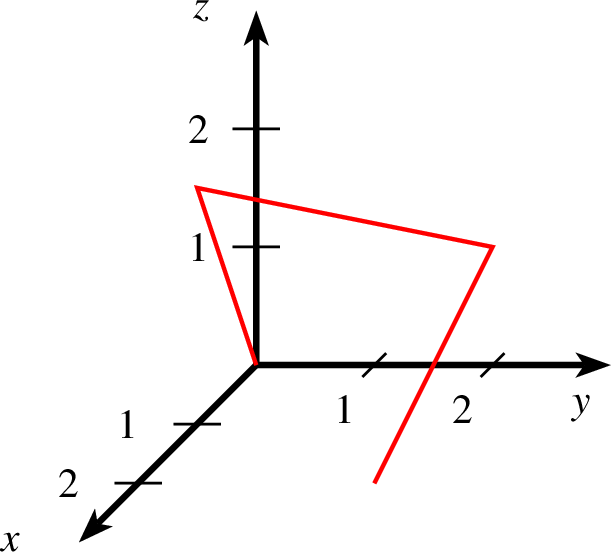
 mit mehreren Wertepaaren
mit mehreren Wertepaaren