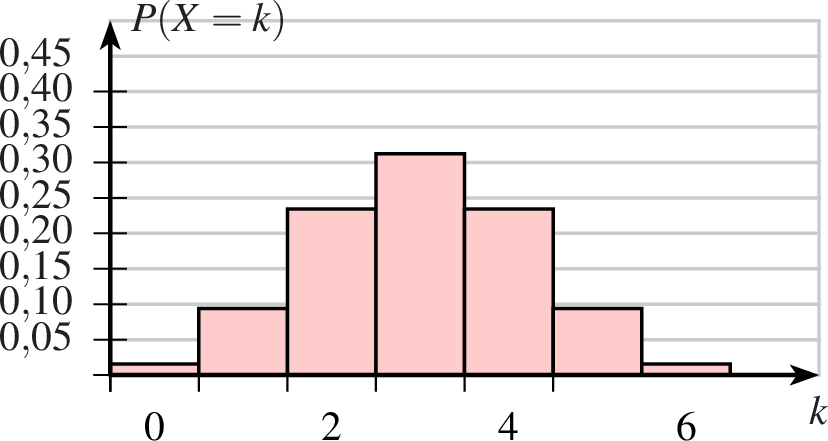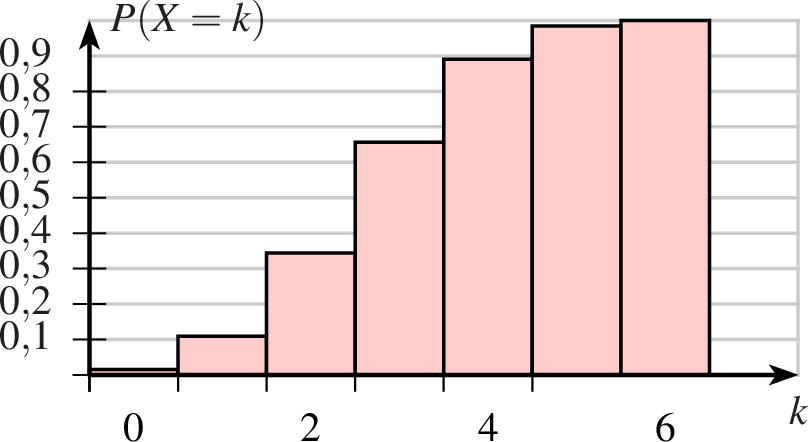7 Diagramme
- Säulen- und Balkendiagramme
- Kreis- und Ringdiagramme
- Piktogramme und Strichlisten
- Eine Legende
- Die Binomialverteilung
Da im Unterricht doch häufiger verschiedene Diagrammtypen auftauchen, habe ich vor etwa einem Jahr mehrere Funktionalitäten in mein Skript eingebaut. Hierzu gehören u.a. die Säulen- und Balkendiagramme, sowie Piktogramme und weitere Diagrammtypen.
7.1 Säulen- und Balkendiagramme
Um Zahlen auf einen Blick zu zeigen und zu erfassen, werden
verschiedene Diagramme verwendet. Hierzu werden häufig Säulen- oder
Balkendiagramme genutzt, die sich nur darin unterscheiden, dass die
Datenreihe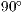 
gedreht ist. Im Folgenden wird zunächst nur das
Säulendiagramm beschrieben. Analoges gilt für das
Balkendiagramm. Über die jeweilige Merkmalsausprägung wird eine
Säule gezeichnet, deren Höhe der absoluten oder relativen Häufigkeit
entspricht.1.
7.1.1 Säulendiagramme
Zunächst einmal die beiden Möglichkeiten für das saeulendiagramm:
saeulendiagramm
[layer=<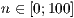 
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (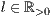 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
p=<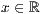 
>,< 
>
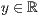[r=<Standardbreite der Säulen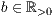 
>,<Standardabstand zur nächsten Säule 
>]
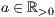ausrichtung=<Textwinkel in Grad>,<Textabstand in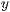 
-Richtung>
<Absoluter Wert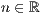 
> (beliebig oft)
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (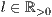 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
[r=<Standardbreite der Säule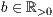 
>,<Standardabstand zur nächsten Säule 
>]
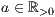text="<Text>"
ende
Dabei steht p für die Startposition der ersten Säule, die
zweite Säule wird im Abstand abstand nach rechts
gezeichnet. breite gibt die Breite der Säule an. Ist bei dem
absoluten Wert keine Farbe, etc. gesetzt, so wird die Säule mit den
vordefinierten Parametern gezeichnet.
Hierbei fallen zwei Parameter auf. Ist achsen gesetzt, so
wird automatisch ein Koordinatensystem mit gezeichnet. Ist
relativ gesetzt, so werden nicht die absoluten Häufigkeiten
dargestellt, sondern die relativen Häufigkeiten. Der Befehl
mitte setzt die Achsenbeschriftung jeweils in die Mitte der
einzelnen Achsen. Der Befehl achsenmarkierung setzt die
Achsenbeschriftung für die einzelnen Achsen.
Im einzelnen lautet er wie folgt:
achsenmarkierung
[x="<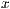 
-Achsenbeschriftung>"]
[y="<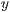 
-Achsenbeschriftung>"]
Alternativ kann man die Position einer einzelnen Säule angeben:
saeulendiagramm
[layer=<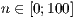 
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (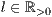 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
[r=<Standardbreite der Säulen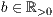 
>]
ausrichtung=<Textwinkel in Grad>,<Textabstand in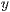 
-Richtung>
< 
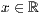><Absoluter Wert 
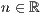> (beliebig oft)
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (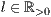 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
[r=<Standardbreite der Säulen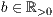 
>]
text="<Text>"
ende
Hier einmal die Beschreibung für das Zeichnen der Säule:
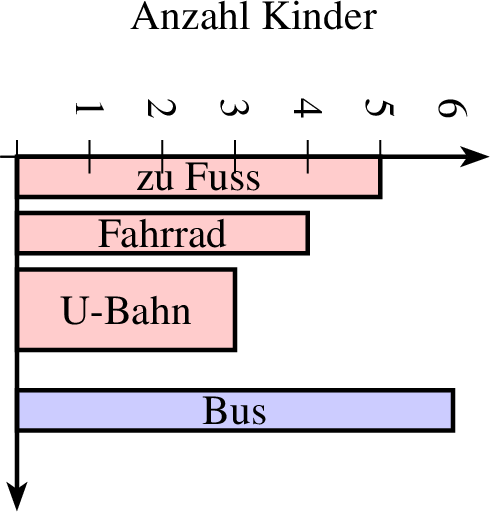
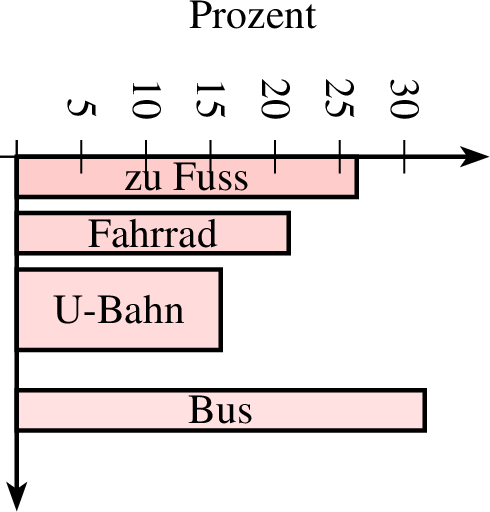
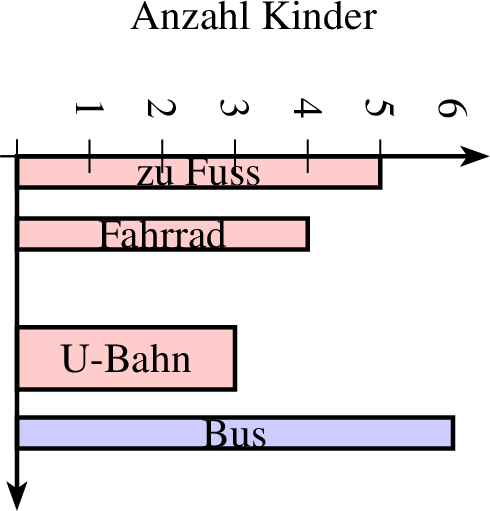
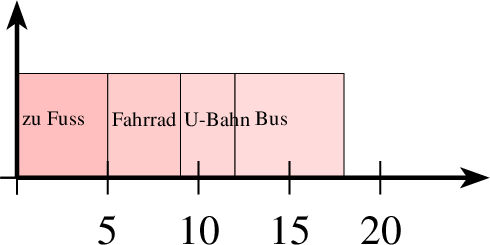
Mit farbverlauf werden die Säulen in Abstufungen mit der gesetzten Füllfarbe gezeichnet. Als Beispiel zeigt die folgende Tabelle die Verkehrsmittel mit denen einzelne Kinder einer Klasse zur Schule kommen und anschließend mehrere Beispiele für Säulendiagrammee.
| Verkehrsmittel | zu Fuß | Fahrrad | U-Bahn | Bus |
| Absolute Häufigkeiten | 5 | 4 | 3 | 6 |
| Relative Häufigkeiten | 5/18 | 4/18 | 3/18 | 6/18 |
Beispiele
| saeulendiagramm-ptxt.ptxt |
|---|
| 1 groesse x=3 y=4 2 achsenmarkierung y="Anzahl Kinder" 3 saeulendiagramm farbe=black,solid,red!20 linie=1,solid parameter="" p=0,0 r=0.5,0.2 ausrichtung=90,mitte 4 5 text="zu Fuss" 5 4 text="Fahrrad" 6 3 r=1,0.5 text="U-Bahn" 7 6 farbe=black,solid,blue!20 text="Bus" 8 ende 9 achsen 10 mitte |
| saeulendiagramm-2-ptxt.ptxt |
|---|
| 1 relativ 2 farbverlauf 3 groesse x=3 y=4 4 achsenmarkierung y="Anzahl Kinder" 5 saeulendiagramm farbe=black,solid,red!20 linie=1,solid parameter="" p=0,0 r=0.5,0.2 ausrichtung=90,mitte 6 5 text="zu Fuss" 7 4 text="Fahrrad" 8 3 r=1,0.5 text="U-Bahn" 9 6 farbe=black,solid,blue!20 text="Bus" 10 ende 11 achsen 12 mitte |
| saeulendiagramm-3-ptxt.ptxt |
|---|
| 1 groesse x=3 y=4 2 achsenmarkierung y="Anzahl Kinder" 3 saeulendiagramm farbe=black,solid,red!20 linie=1,solid parameter="" r=0.5 ausrichtung=90,mitte 4 1,5 text="zu Fuss" 5 2,4 text="Fahrrad" 6 4,3 r=1 text="U-Bahn" 7 5.2,6 farbe=black,solid,blue!20 text="Bus" 8 ende 9 achsen 10 mitte |
7.1.2 Balkendiagramme
Analog zum Säulendiagramm gibt es das Balkendiagramm
Hier die erste Syntax des balkendiagramm:
balkendiagramm
[layer=<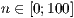 
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (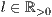 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
p=<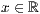 
>,< 
>
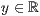r=<Standardhöhe der Säulen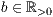 
>,<Standardabstand zur nächsten Säule 
>
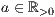<Absoluter Wert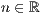 
> (beliebig oft)
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (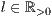 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
r=<Standardhöhe der Säulen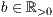 
>,<Standardabstand zur nächsten Säule 
>
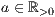text="<Text>"
ende
Dabei steht p für die Startposition des ersten Balkens, die
zweite Säule wird im Abstand abstand nach oben
gezeichnet. hoehe gibt die Höhe des Balkens an.
Die zweite Syntax lautet
balkendiagramm
[layer=<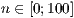 
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (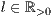 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
r=<Standardhöhe der Säulen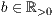 
>
<Absoluter Wert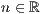 
>,< 
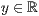> (beliebig oft)
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (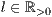 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
r=<Standardhöhe der Säulen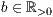 
>
text="<Text>"
ende
Beispiele
| balkendiagramm-ptxt.ptxt |
|---|
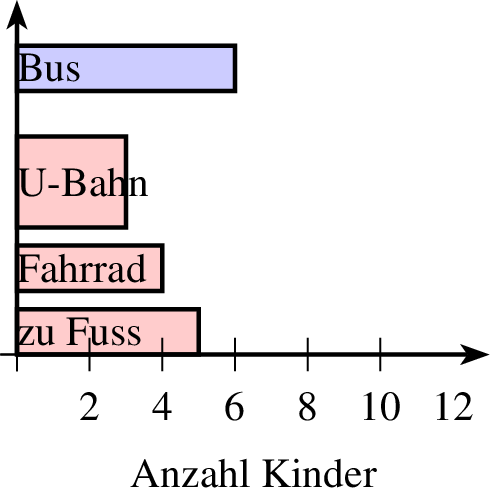
| 1 groesse x=4 y=3 2 achsenmarkierung x="Anzahl Kinder" 3 balkendiagramm farbe=black,solid,red!20 linie=1,solid parameter="" p=0,0 r=0.5,0.2 ausrichtung=0,auf 4 5 text="zu Fuss" 5 4 text="Fahrrad" 6 3 r=1,0.5 text="U-Bahn" 7 6 farbe=black,solid,blue!20 text="Bus" 8 ende 9 achsen 10 mitte |
| balkendiagramm-2-ptxt.ptxt |
|---|
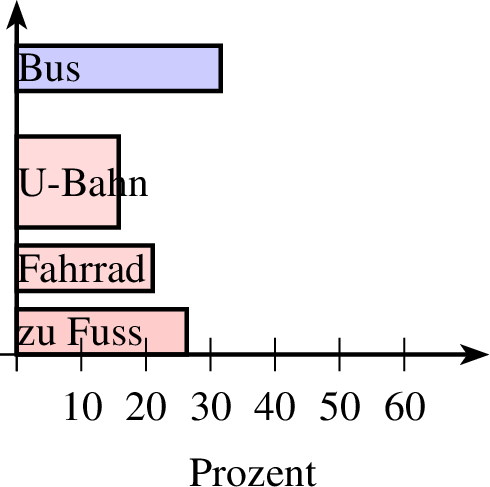
| 1 relativ 2 farbverlauf 3 groesse x=4 y=3 4 achsenmarkierung x="Anzahl Kinder" 5 balkendiagramm farbe=black,solid,red!20 linie=1,solid parameter="" p=0,0 r=0.5,0.2 ausrichtung=0,auf 6 5 text="zu Fuss" 7 4 text="Fahrrad" 8 3 r=1,0.5 text="U-Bahn" 9 6 farbe=black,solid,blue!20 text="Bus" 10 ende 11 achsen 12 mitte |
| balkendiagramm-3-ptxt.ptxt |
|---|
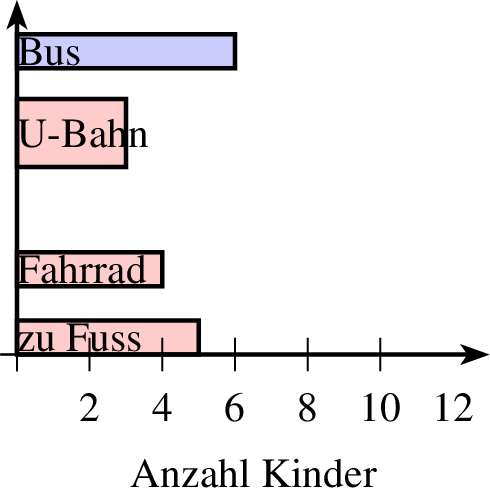
| 1 groesse x=4 y=3 2 achsenmarkierung x="Anzahl Kinder" 3 balkendiagramm farbe=black,solid,red!20 linie=1,solid parameter="" r=0.5 ausrichtung=0,auf 4 5,1 text="zu Fuss" 5 4,2 text="Fahrrad" 6 3,4 r=1 text="U-Bahn" 7 6,5.2 farbe=black,solid,blue!20 text="Bus" 8 ende 9 achsen 10 mitte |
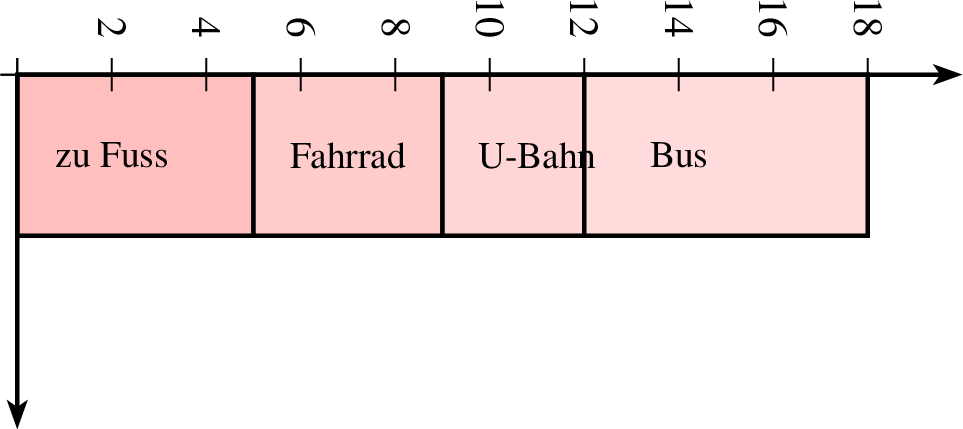
7.1.3 Gestapelte Säulen- und Balkendiagramme
In einem gestapelten Diagramm werden Werte mehrerer Datenreihen jeweils aufeinander oder nebeneinander gestapelt dargestellt. Der Gesamtbalken ist jeweils der Gesamtwert. Dabei sind die Änderungen zum Säulen- ud Balkendiagramm minimal. Anstelle von saeulendiagramm wird saeulendigrammgestapelt genutzt. Analog ist dies beim balkendiagramm der Befehl balkendiagrammgestapelt. Beispiele dazu sind in den Abbildungen 7.1.3 und 7.1.3 zu sehen.
| balkendiagramm-gestapelt-ptxt.ptxt |
|---|
| 1 beschriftunggroesse "tiny" 2 farbverlauf 3 groesse x=4 y=1.5 4 balkendiagrammgestapelt farbe=black,solid,red!22 linie=0.2,solid p=0,0 r=1,5 ausrichtung=0,2 5 5 text="zu Fuss" 6 4 text="Fahrrad" 7 3 text="U-Bahn" 8 6 text="Bus" 9 ende 10 achsen |
| saeulendiagramm-gestapelt-ptxt.ptxt |
|---|
| 1 beschriftunggroesse "small" 2 groesse x=3 y=8 3 farbverlauf 4 saeulendiagrammgestapelt farbe=black,solid,red!20 linie=1,solid p=0,0 r=1,5 ausrichtung=90,2 5 5 text="zu Fuss" 6 4 text="Fahrrad" 7 3 text="U-Bahn" 8 6 text="Bus" 9 ende 10 achsen |
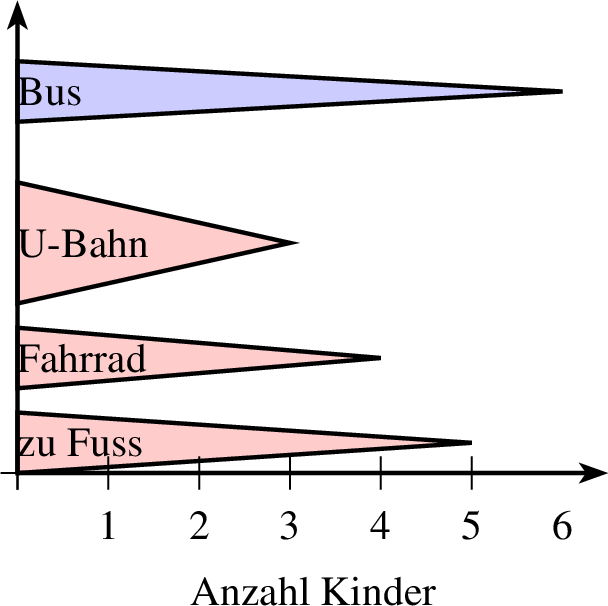
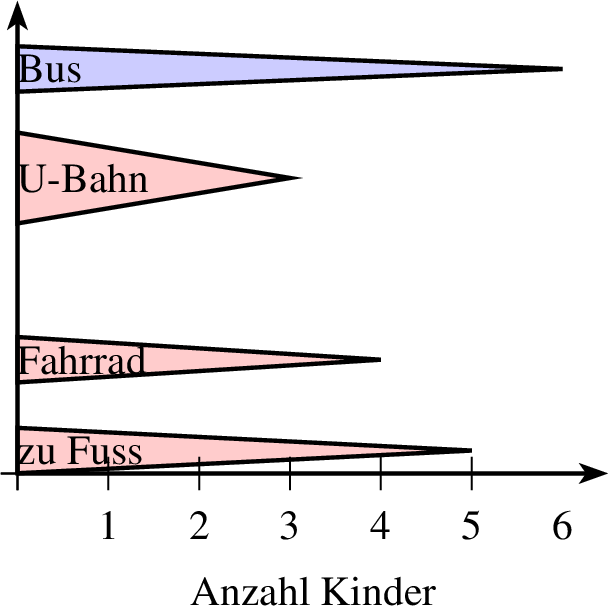
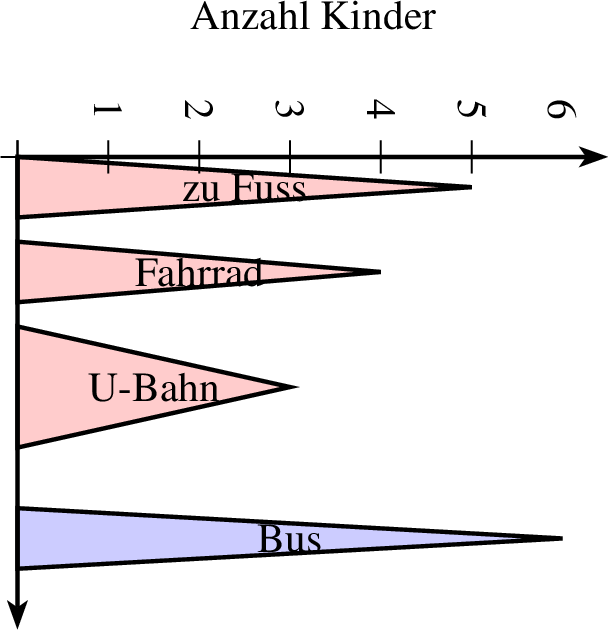
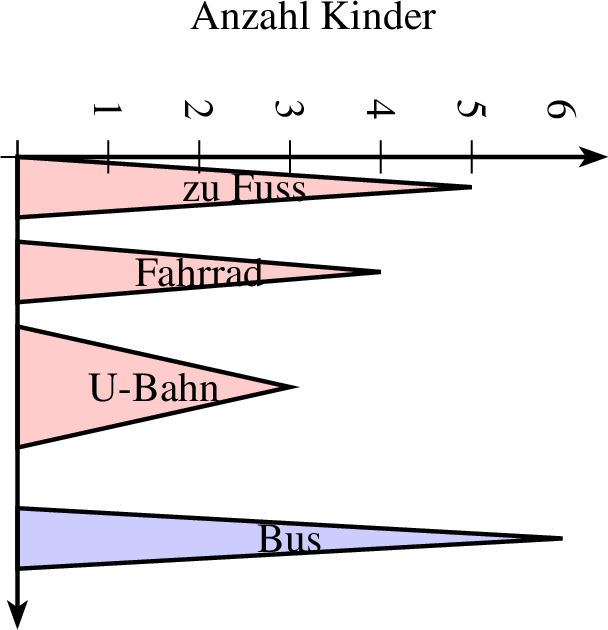
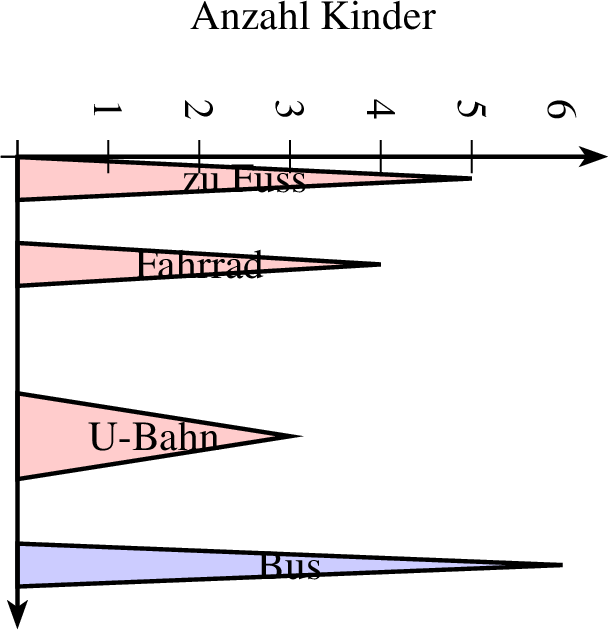
7.1.4 Weitere Säulen- und Balkendiagrammtypen
Zu guter Letzt gibt es noch die Säulen- und Balkendiagramme in Form von Dreiecken. Dazu wird fast der gleiche Befehl genutzt wie in 7.1.1 und 7.1.1, nur dass statt saeulendiagramm in Zeile 2 der Befehl saeulendiagrammdreieck steht. r steht dabei für die Breite eines gleichschenkligen Dreiecks.
| balkendiagramm-dreieck-ptxt.ptxt |
|---|
| 1 groesse x=5 y=4 2 achsenmarkierung x="Anzahl Kinder" 3 balkendiagrammdreieck farbe=black,solid,red!20 linie=1,solid parameter="" p=0,0 r=0.5,0.2 ausrichtung=0,auf 4 5 text="zu Fuss" 5 4 text="Fahrrad" 6 3 r=1,0.5 text="U-Bahn" 7 6 farbe=black,solid,blue!20 text="Bus" 8 ende 9 achsen 10 mitte |
| balkendiagramm-dreieck-2-ptxt.ptxt |
|---|
| 1 relativ 2 farbverlauf 3 groesse x=5 y=4 4 achsenmarkierung x="Anzahl Kinder" 5 balkendiagrammdreieck farbe=black,solid,red!20 linie=1,solid parameter="" p=0,0 r=0.5,0.2 ausrichtung=0,auf 6 5 text="zu Fuss" 7 4 text="Fahrrad" 8 3 r=1,0.5 text="U-Bahn" 9 6 farbe=black,solid,blue!20 text="Bus" 10 ende 11 achsen 12 mitte |
| balkendiagramm-dreieck-3-ptxt.ptxt |
|---|
| 1 groesse x=5 y=4 2 achsenmarkierung x="Anzahl Kinder" 3 balkendiagrammdreieck farbe=black,solid,red!20 linie=1,solid parameter="" r=0.5 ausrichtung=0,auf 4 5,1 text="zu Fuss" 5 4,2 text="Fahrrad" 6 3,4 r=1 text="U-Bahn" 7 6,5.2 farbe=black,solid,blue!20 text="Bus" 8 ende 9 achsen 10 mitte |
| saeulendiagramm-dreieick-ptxt.ptxt |
|---|
| 1 groesse x=4 y=5 2 achsenmarkierung y="Anzahl Kinder" 3 saeulendiagrammdreieck farbe=black,solid,red!20 linie=1,solid parameter="" p=0,0 r=0.5,0.2 ausrichtung=90,mitte 4 5 text="zu Fuss" 5 4 text="Fahrrad" 6 3 r=1,0.5 text="U-Bahn" 7 6 farbe=black,solid,blue!20 text="Bus" 8 ende 9 achsen 10 mitte |
| saeulendiagramm-dreieick-2-ptxt.ptxt |
|---|
| 1 relativ 2 farbverlauf 3 groesse x=4 y=5 4 achsenmarkierung y="Anzahl Kinder" 5 saeulendiagrammdreieck farbe=black,solid,red!20 linie=1,solid parameter="" p=0,0 r=0.5,0.2 ausrichtung=90,mitte 6 5 text="zu Fuss" 7 4 text="Fahrrad" 8 3 r=1,0.5 text="U-Bahn" 9 6 farbe=black,solid,blue!20 text="Bus" 10 ende 11 achsen 12 mitte |
| saeulendiagramm-dreieick-3-ptxt.ptxt |
|---|
| 1 groesse x=4 y=5 2 achsenmarkierung y="Anzahl Kinder" 3 saeulendiagrammdreieck farbe=black,solid,red!20 linie=1,solid parameter="" r=0.5 ausrichtung=90,mitte 4 1,5 text="zu Fuss" 5 2,4 text="Fahrrad" 6 4,3 r=1 text="U-Bahn" 7 5.5,6 farbe=black,solid,blue!20 text="Bus" 8 ende 9 achsen 10 mitte |
7.2 Kreis- und Ringdiagramme
Die bisherigen Diagrammtypen waren alles Achsendiagramme, nun sollen noch weitere Diagrammtypen behandelt werden.
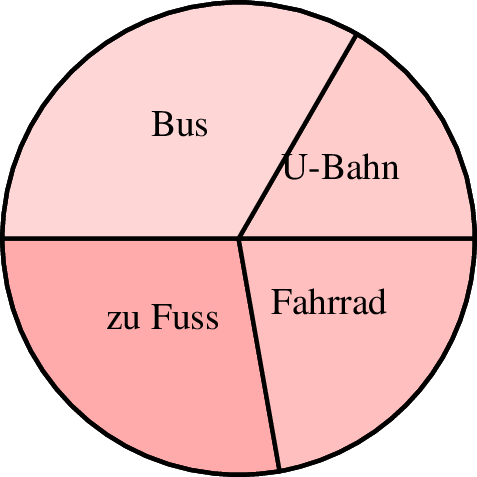
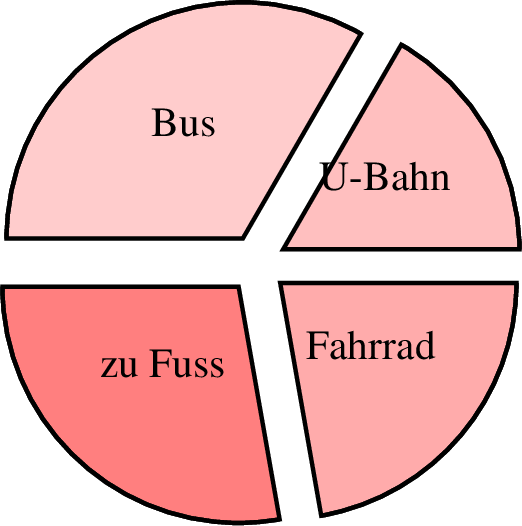
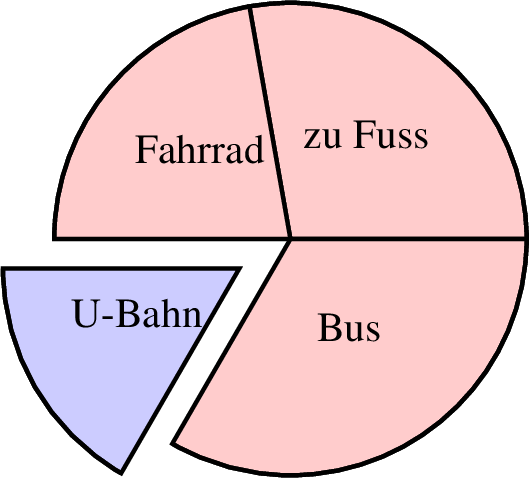
7.2.1 Torten- oder Kreisdiagramm
Zunächst soll ein Tortendiagramm oder auch Kreisdiagramm
behandelt werden. 2 Dabei steht dann ein
Kresisektor für einen Teilwert und der gesamte Kreis für die
Gesamtsumme aller Teilwerte.
Der Befehl tortendiagramm wird wie gewohnt aufgerufen.
tortendiagramm
[layer=<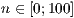 
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (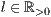 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
p=<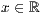 
>,< 
>
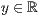r=<Radius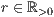 
>,<Abstand Mittelpunkt 
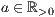>,<Startwinkel in Grad>
<Absoluter Anteil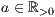 
>
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (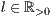 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
[r=<Radius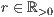 
>,<Abstand Mittelpunkt 
>]
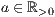text="<Text>"
ende
| kreisdiagramm-ptxt.ptxt |
|---|
| 1 farbverlauf 2 beschriftunggroesse "small" 3 tortendiagramm farbe=black,solid,red!20 linie=1,solid p=0,0 r=2,0,180 4 5 text="zu Fuss" 5 4 text="Fahrrad" 6 3 text="U-Bahn" 7 6 text="Bus" 8 ende |
p steht dabei für den Mittelpunkt des
Kreises. r=2,0,180 steht dabei für den Radius des
Kreises mit 2 und 0 steht dafür, wie weit der Abstand vom Mittelpunkt
ist. 180 ist der Winkel, auf dem der erste Kreissektor beginnt. Die
weiteren Sektoren werden immer gegen den Uhrzeigersinn angeordnet.
Beispiele
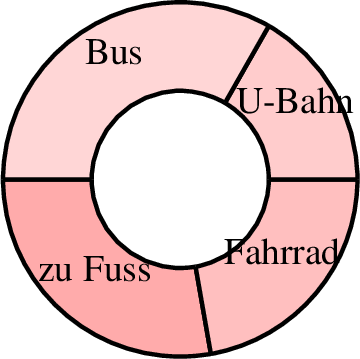
7.2.2 Ringdiagramm
Ein weiterer Diagrammtyp ist das Ringdiagramm.
ringdiagramm
[layer=<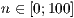 
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (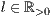 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
p=<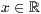 
>,< 
>
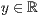r=<Außenradius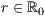 
>,<Ringbreite 
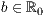>,<Startwinkel in Grad>
<Absoluter Anteil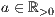 
>
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (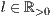 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
[r=<Radius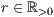 
>,<Abstand Mittelpunkt 
>]
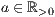text="<Text>"
ende
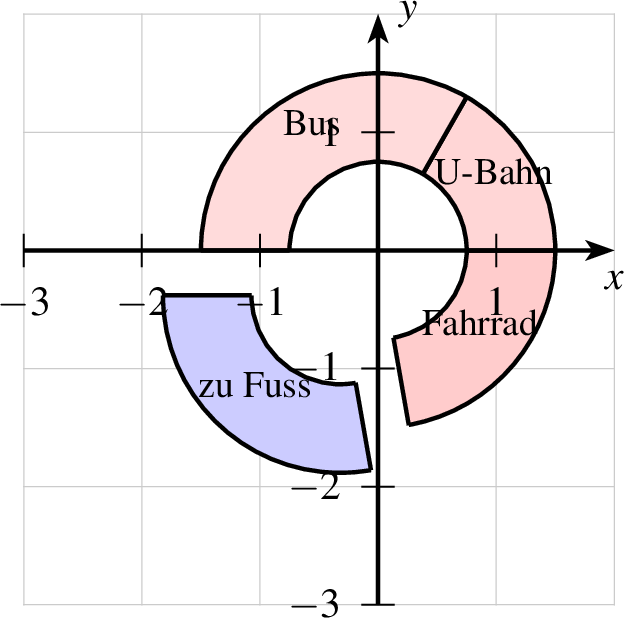
Dies wird mit dem Befehl ringdiagramm aufgerufen, der
ansonsten analog zum Kreisdiagrammbefehl ist. Hierbei ist allerdings
im Befehl r die erste Zahl der Außenradius des Kreises und
die zweite Zahl die Breite des Ringes dar.
| ringdiagramm-ptxt.ptxt |
|---|
| 1 farbverlauf 2 beschriftunggroesse "small" 3 ringdiagramm farbe=black,solid,red!20 linie=1,solid p=0,0 r=1.5,0.75,180 4 5 text="zu Fuss" 5 4 text="Fahrrad" 6 3 text="U-Bahn" 7 6 text="Bus" 8 ende |
In der Abbildung 7.2.2 sieht man eine kleine Änderung im Befehl r. Auch hier ist die erste Zahl der Außenradius und die zweite Zahl die Breite des Ringausschnittes. Die dritte Zahl sthet für den Abstand vom Mittelpunkt p.
7.3 Piktogramme und Strichlisten
Als zwei weitere Diagrammtypen habe ich noch ein Piktogramm und eine Strichliste realisiert.
7.3.1 Piktogramm
In einem Piktogramm werden absolute Häufigkeiten und Größen
visualiert. Dabei entspricht jedes Symbol einer bestimmten Anzahl
bzw. Größe. Mit dem Befehl bilddiagramm wird ein Piktogramm
erstellt.
piktogramm
p=<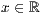 
>,< 
>
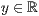r=<Breite des Bildes in pt>,<Winkel des Bildes in Grad>,<Abstand in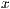 
-Richtung>,<Abstand in 
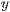-Richtung zum nächsten Bild>
ausrichtung=<Textwinkel in Grad>,<Ausrichtung in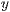 
-Richtung>
<Anzahl der http://www.xenia-rendtel.de/Download/Plotter/Bilder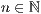 
> beliebig oft
[r=<Breite des Bildes in pt>,<Winkel des Bildes in Grad>,<Abstand in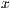 
-Richtung>,<Abstand in 
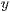-Richtung zum nächsten Bild>]
text="<Text>"
[ausrichtung=<Textwinkel in Grad>,<Ausrichtung in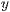 
-Richtung>]
"<Dateiname>"
ende
Dabie steht p für den Startpunkt des ersten Bildes. In
r steht zunächst die Breite eines Bildes, der Offset und der
Abstand der http://www.xenia-rendtel.de/Download/Plotter/Bilder in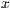 
und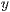 
Richtung. In der
ausrichtung kann der Winkel des Textes und der Abstand in
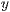-Richtung definiert werden.
| piktogramm-ptxt.ptxt |
|---|
| 1 piktogramm p=0.2,0.5 r=0.5,0,1,0.5 ausrichtung=0,-2 2 5 text="zu Fuss" "Abbildungen/fuss.eps" 3 4 r=1,45,0.5,1 text="Rad" "Abbildungen/rad.eps" 4 3 text="Zug" ausrichtung=90,-1 "Abbildungen/zug.eps" 5 6 text="Bus" "Abbildungen/bus.eps" 6 ende |
7.3.2 Eine Strichliste
Auch eine Strichliste habe ich in meinem Skript realisiert. Mit
dem Befehl strichliste fängt dieser an.
strichliste
[layer=<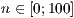 
>]
p=<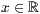 
>,< 
>
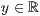r=<Höhe des Striches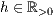 
>,<Abstand in 
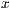-Richtung 
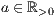><Anzahl Striche 
>
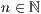In r wird die Höhe und der horizontale Abstand
definiert. Die Anzahl gibt an, wie viele Striche gezeichnet werden
sollen.
| strichliste-ptxt.ptxt |
|---|
| 1 strichliste linie=2,solid,black p=0,0 r=1,0.2 17 |
7.4 Eine Legende
Wenn man ein Diagramm zeichnen möchte, darf natürlich keine
Legende fehlen. Dies wird mit dem Befehl legende
aufgerufen. Die genaue Syntax lautet:
legende
[layer=<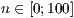 
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (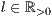 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
p=<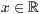 
>,< 
>
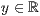r=<Breite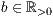 
>,<Höhe 
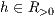>,<Abstand in 
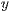-Richtung 
>
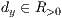text="<Text>"
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (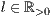 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
ende
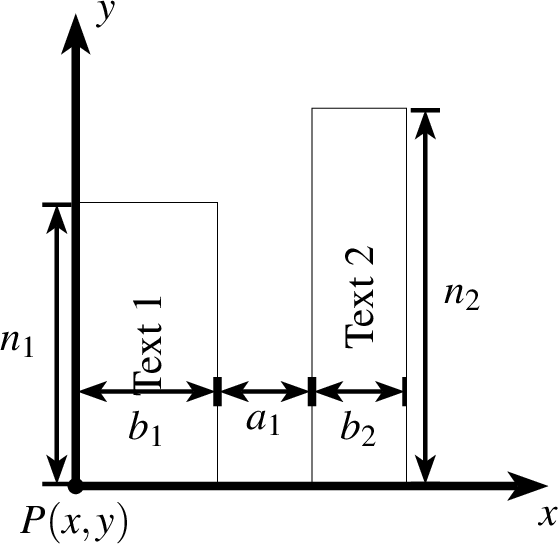
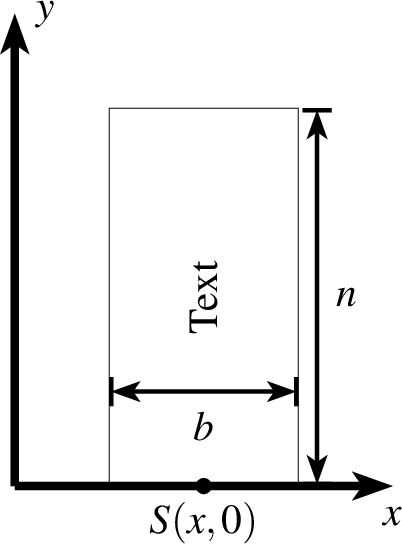
p steht für die Startposition des ersten Eintrages. Die
Breite und Höhe gibt die Ausmaße des Rechteckes an. Der letzte Eintrag
steht für den Abstand zwischen den Rechtecken in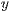 
-Richtung. Die
weiteren Rechtecke werden von oben nach unten gezeichnet.
| legende-ptxt.ptxt |
|---|
| 1 legende farbe=red,solid,red!20 linie=1,solid p=0,0 r=0.5,0.5,0.2 2 text="zu Fuss" farbe=black,solid,green!20 linie=2,solid 3 text="Rad" farbe=black,solid,red!20 4 text="Zug" farbe=black,solid,blue!20 5 text="Bus" farbe=black,solid,orange!20 6 ende |
| legende-2-ptxt.ptxt |
|---|
| 1 farbverlauf 2 legende farbe=black,solid,red!20 linie=1,solid p=0,0 r=0.5,0.5,0.2 3 text="zu Fuss" 4 text="Rad" 5 text="Zug" 6 text="Bus" 7 ende |
7.5 Die Binomialverteilung
In meinem Skript habe ich ebenfalls die Binomialverteilung
realisiert. Eine Zufallsgröße heißt binomialverteilt mit den
Parametern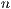 
und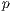 
, wenn für alle 
( 
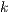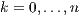) gilt:
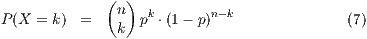
7.5.1 Die Binomialvertielung als Säulendiagramm
Die Syntax des Skriptes sieht dabei wie folgt aus:
binomial
[layer=<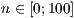 
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (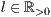 
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
np=<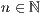 
>,< 
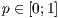>,<ja|nein>
b=<Säulenbreite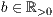 
>,< 
>
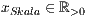Dabei steht ja oder nein dafür, ob die
Binomialverteilung aufsummiert werden soll oder nicht. Setzt man
ja, so wird die kumulierte Binomialverteilung
dargestellt. Desweiteren kann die
Säulenbreite und der Abstand der Achsenmarkierung festgelegt werden.
Setzt man auch hier erneut achsen mit als Befehl, so werden die
Achsen mit gezeichnet.
| binomial-ptxt.ptxt |
|---|
| 1 achsenmarkierung x="$k$" y="$P(X=k)$" 2 groesse x=6 y=3 3 achsen 4 gitter 5 binomial farbe=black,solid,red!20 linie=0.8,solid np=6,0.5,nein b=1,2 6 7 8 |
| binomial-kum-ptxt.ptxt |
|---|
| 1 achsenmarkierung x="$k$" y="$P(X=k)$" 2 groesse x=6 y=3 3 achsen 4 gitter 5 binomial farbe=black,solid,red!20 linie=0.8,solid np=6,0.5,ja b=1,2 6 7 8 |
binomialteil
[layer=<
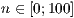>][farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (
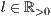)>,<Linienart>][parameter="<Pstricksbefehle>"]
np=<
>,< 
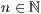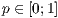>,<Startwert 
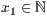>,<Endwert 
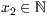><ja|nein>b=<Säulenbreite
>,< 
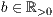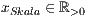>Hierbei wird
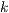von startwert bis endwert dargestellt.
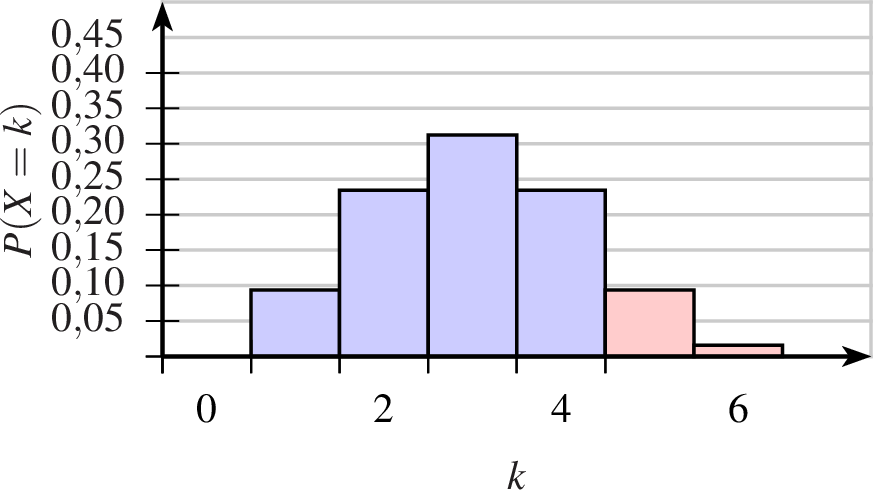
| binomial-teil-ptxt.ptxt |
|---|
| 1 achsenmarkierung x="$k$" y="$P(X=k)$" 2 groesse x=6 y=3 3 achsen 4 gitter 5 mitte 6 binomialteil farbe=black,solid,blue!20 linie=0.8,solid np=6,0.5,1,4,nein b=1,2 7 binomialteil farbe=black,solid,red!20 linie=0.8,solid np=6,0.5,5,6,nein b=1,2 8 9 |
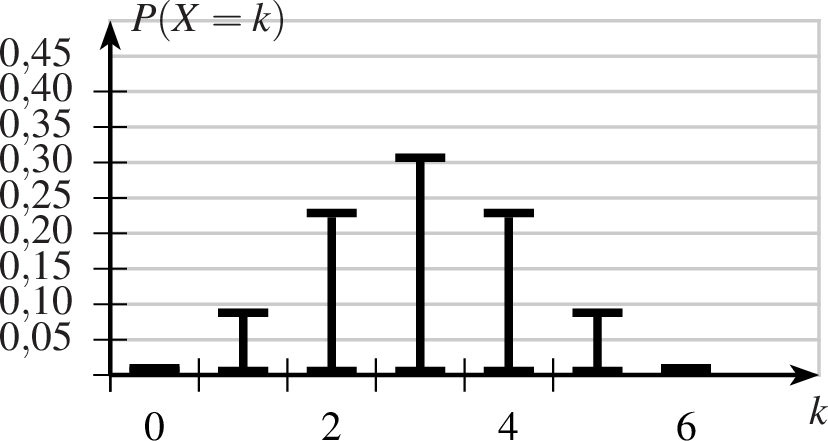
7.5.2 Die Binomialvertielung als Strichdiagramm
Analog zu den Befehlen binomial und binomialteil gibt es dei Befehle binomialstrich und binomialteilstrich, die anstelle von Säulen nur Striche zeichnen.
| binomialstrich-ptxt.ptxt |
|---|
| 1 achsenmarkierung x="$k$" y="$P(X=k)$" 2 groesse x=6 y=3 3 achsen 4 gitter 5 binomialstrich linie=2,solid np=6,0.5,nein b=1,2 6 7 8 |
- 1
- Siehe [Div., 2010]
- 2
- Im Folgenden wird sich weiterhin auf die Tabelle 7.1.1 bezogen.