


6 Plotten von Funktionen und Daten
- Funktionen zeichnen
- Markierungen an Graphen
- Ableitungen zeichnen
- Tangenten und Tangentendreiecke
- Sekanten und Sekantendreiecke
- Stammfunktionen und Integrale
- Rotationskörper um die
 -Achse
-Achse
- Parametrisierte Kurven
- Zeichnen von Funktionsfolgen
- Plotten von Daten
In meinem Skript habe ich die Möglichkeit realisiert Funktionen und Daten zu zeichnen. Dabei werden im Hintergrund einige Berechnungen angestellt, die einem das Leben vereinfachen.
6.1 Funktionen zeichnen
Um Funktionen zu zeichnen habe ich den Befehl graph geschrieben. Die Syntax ist die folgende:
graph
[layer=<  >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=<  >,<
>,<  > [y=<
> [y=<  >,<
>,<  >]
>]
<Funktionsterm  >
>
Hierbei wird der Funktionsterm mit der Variablen  in der algebraischen
Notation erwartet. Sind ymin und ymax nicht gesetzt, so
wird die Funktion in den Grenzen xmin und xmax
gezeichnet. Ist dies angegeben, so ist die Funktion auf diesen Bereich
beschränkt.
in der algebraischen
Notation erwartet. Sind ymin und ymax nicht gesetzt, so
wird die Funktion in den Grenzen xmin und xmax
gezeichnet. Ist dies angegeben, so ist die Funktion auf diesen Bereich
beschränkt.
| graph-ptxt.ptxt |
|---|
| 1 achsen 2 graph layer=50 farbe=black linie=1,solid parameter="" x=-3,3 y=-2,3 x^3+1 |
6.2 Markierungen an Graphen
Möchte man eine Markierung an einer Funktion oder eine generelle Markierung
von einem Wertepaar  zeichnen, so steht einem der Befehl
graphmarkierung zur Verfügung.
zeichnen, so steht einem der Befehl
graphmarkierung zur Verfügung.
graphmarkierung
[layer=<  >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>,"<x|y|xy>"]
)>,<Linienart>,"<x|y|xy>"]
[parameter="<Pstricksbefehle>"]
x=<  >
>
[y=<  >]
>]
[text=<"Text an der  -Achse">,<"Text an der
-Achse">,<"Text an der  -Achse">]
-Achse">]
[<Funktionsterm  >] wenn y nicht definiert
>] wenn y nicht definiert
Standardmäßig wird der Befehl xy bei der linie genutzt.
| graphmarkierung-ptxt.ptxt |
|---|
| 1 achsen 2 graph layer=50 farbe=black linie=1,solid parameter="" x=-4,4 y=-2,2 1.5*sin(x) 3 graphmarkierung farbe=red linie=1,solid,x x=1.5 text="$x_1$","$y_1$" 1.5*sin(x) 4 graphmarkierung farbe=blue linie=2,dashed,y x=-2.3 text="$x_2$","$y_2$" 1.5*sin(x) 5 graphmarkierung x=3 y=-1.5 text="$x_3$","$y_3$" |
6.3 Ableitungen zeichnen
Um Ableitungen  zu zeichnen gibt es den Befehl ableitung, der fast
analog zum Befehl graph ist. Die Syntax lautet:
zu zeichnen gibt es den Befehl ableitung, der fast
analog zum Befehl graph ist. Die Syntax lautet:
ableitung
[layer=<  >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=< 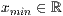 >,<
>,<  > [y=<
> [y=< 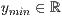 >,<
>,<  >]
>]
<Funktionsterm  >[,<Grad der Ableitung
>[,<Grad der Ableitung  >]
>]
Hierbei kann der Grad der Ableitung angegeben werden. Standardmäßig ist der
Grad auf 1 gesetzt. Zu beachten ist, dass wenn  größer 1 gewählt wird, kann
die Funktion über die
größer 1 gewählt wird, kann
die Funktion über die  -Achse hinaus gezeichnet werden.
-Achse hinaus gezeichnet werden.
| ableitung-ptxt.ptxt |
|---|
| 1 achsen 2 graph layer=50 farbe=black linie=1,solid parameter="" x=-4,4 y=-2,3 x^4+1 3 ableitung layer=50 farbe=red linie=1,solid parameter="" x=-4,4 y=-2,3 x^4+1 |
6.4 Tangenten und Tangentendreiecke
6.4.1 Zeichnen einer Tangente
Die Steigung einer Funktion in einem Punkt wird häufig durch das Zeichnen
eines kurzen Tangentenstückes verdeutlicht. Dies kann durch die Ableitung der
Funktion oder durch die Berechnung einer genügend kleinen Sekante geschehen.
Die Gleichung einer Tangente an der Stelle  für die Funktion
für die Funktion  ist
definiert durch
ist
definiert durch
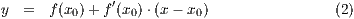
Eine Tangente kann kann nun mit dem Befehl tangente gezeichnet
werden. Die Syntax ist dabei die folgende:
tangente
[layer=<  >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=<  >
>
dx=<  >
>
<Funktionsterm  >
>
Dabei ist  die Stelle, für die die Tangente berechnet werden soll und
die Stelle, für die die Tangente berechnet werden soll und
 die Länge der einzuzeichnenden Tangente.
die Länge der einzuzeichnenden Tangente.
| tangente-ptxt.ptxt |
|---|
| 1 achsen 2 gitter 3 graph linie=1,solid x=-4,4 y=-2,2 sin(x) 4 tangente farbe=red linie=1,solid x=-1 dx=1 sin(x) 5 tangente farbe=blue linie=1,solid x=1.5 dx=2 sin(x) 6 |
6.4.2 Zeichnen eines Tangentendreiecks
Analog zur Tangente gibt es denn Befehl des Tangentendreiecks, der
anstelle der Tangente ein vollständiges Steigungsdreieck einzeichnet.
tangentendreieck
[layer=<  >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=<  >
>
dx=<  >
>
<Funktionsterm  >
>
| tangentendreieck-ptxt.ptxt |
|---|
| 1 achsen 2 gitter 3 graph linie=1,solid x=-4,4 y=-2,2 sin(x) 4 tangentendreieck farbe=red linie=1,solid x=-1 dx=1 sin(x) 5 tangentendreieck farbe=blue linie=1,solid x=1.5 dx=2 sin(x) |
6.5 Sekanten und Sekantendreiecke
6.5.1 Zeichnen von Sekanten
Eine Gerade die durch zwei verschiedene Punkte einer Funktion  geht, nennt
man Sekante. Die Steigung der Sekante durch zwei verschiedene Punkte
geht, nennt
man Sekante. Die Steigung der Sekante durch zwei verschiedene Punkte
 und
und  des Graphen ist gegeben durch
des Graphen ist gegeben durch
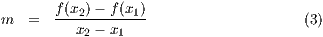
Für mein Skript ist die Syntax der sekante die Folgende:
sekante
[layer=<  >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=<  >
>
dx=<  >
>
<Funktionsterm  >
>
Dabei ergibt sich  durch
durch  .
.
| sekante-ptxt.ptxt |
|---|
| 1 achsen 2 gitter 3 graph linie=1,solid x=-4,4 y=-2,2 sin(x) 4 sekante farbe=red linie=1,solid x=-1 dx=1 sin(x) 5 sekante farbe=blue linie=1,solid x=1.5 dx=2 sin(x) 6 |
6.5.2 Zeichnen eines Sekantendreiecks
Analog zur Sekante gibt es denn Befehl des Sekantendreiecks, der
anstelle der Sekante ein vollständiges Steigungsdreieck zeichnet.
sekantendreieck
[layer=<  >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=< 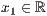 >
>
dx=<  >
>
<Funktionsterm  >
>
| sekantendreieck-ptxt.ptxt |
|---|
| 1 achsen 2 gitter 3 graph linie=1,solid x=-4,4 y=-2,2 sin(x) 4 sekantendreieck farbe=red linie=1,solid x=-1 dx=1 sin(x) 5 sekantendreieck farbe=blue linie=1,solid x=1.5 dx=2 sin(x) |
6.6 Stammfunktionen und Integrale
6.6.1 Stammfunktionen
Um Stammfunktionen zu zeichnen gibt es den Befehl stammfunktion, der fast analog zum Befehl graph ist. Die Syntax lautet:
stammfunktion
[layer=<  >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=<  >,<
>,<  >
>
[y=<  >,<
>,<  >]
>]
[nullwert=<  >]
>]
<Funktionsterm  >
>
Dabei stellt nullwert die additive Konstante der Stammfunktion dar.
| stammfunktion-ptxt.ptxt |
|---|
| 1 achsen 2 graph linie=1,solid x=-4,4 y=-2,3 x^4+1 3 stammfunktion farbe=red linie=1,solid x=-4,4 y=-2,3 x^4+1 |
6.6.2 Flächen unter einer Funktion
Hinführend auf das Integral ergibt sich natürlich auch die Obersumme und
Untersumme einer Funktion. Dabei betrachtet man die (beschränkte)
Funktion  , wobei
, wobei  und
und  gilt. Wird nun das
Intervall
gilt. Wird nun das
Intervall 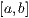 in
in  Teile zerlegt mit
Teile zerlegt mit  ,
so ist die Ober- bzw. Untersumme definiert als
,
so ist die Ober- bzw. Untersumme definiert als
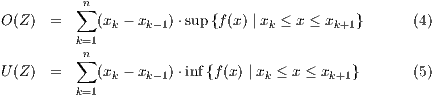
Dies ist nun mit dem Befehl oberuntersumme realisiert. Die Syntax
sieht dabei wie folgt aus:
oberuntersumme
[layer=<  >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=<  >,<
>,<  >
>
[y=< 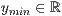 >,<
>,<  >]
>]
n=<Einteilung  >
>
summen=<ober|unter|beide>
<Funktionsterm  >
>
Dabei steht ober dafür, dass die Obersumme gezeichnet wird,
unter zeichnet die Untersumme und beide zeichnet beide Treppenfunktionen. Ist  nicht gesetzt, so wird die Treppenfunktion zwischen
nicht gesetzt, so wird die Treppenfunktion zwischen  und
und  direkt gezeichnet. Ansonsten werden diese Werte aufgrund der
direkt gezeichnet. Ansonsten werden diese Werte aufgrund der  -Werte angepasst.
-Werte angepasst.
| oberuntersumme-ptxt.ptxt |
|---|
| 1 achsen 2 graph layer=61 farbe=black linie=1,solid x=-4,4 y=0,4 (0.5*x)^2 3 oberuntersumme farbe=red,solid,red!20 linie=1,solid x=-4,4 y=0,4 n=6 summen=ober (0.5*x)^2 |
| oberuntersumme-2-ptxt.ptxt |
|---|
| 1 achsen 2 graph layer=61 farbe=black linie=1,solid x=-4,4 y=0,3 (0.5*x)^2 3 oberuntersumme farbe=red,solid,red!20 linie=1,solid x=-4,4 y=0,3 n=6 summen=unter (0.5*x)^2 |
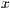 -Achse in dem angegebenen Intervall. Die Syntax ist:
-Achse in dem angegebenen Intervall. Die Syntax ist:integral
[layer=<
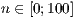 >]
>][farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (
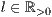 )>,<Linienart>]
)>,<Linienart>][parameter="<Pstricksbefehle>"]
x=<
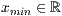 >,<
>,< 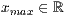 >
>[y=<
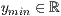 >,<
>,< 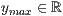 >]
>]<Funktionsterm
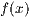 >
>Ist y nicht angegeben, so werden die Grenzen automatisch berechnet.
| integral-ptxt.ptxt |
|---|
| 1 achsen 2 integral layer=5 farbe=red!20,solid,red!20 linie=1,solid x=-3,3 y=-1.5,1.5 cos(2*x) |
6.6.3 Einschlußzwischen zwei Funktionen
Beschäftigt man sich mit dem Integral, so soll natürlich auch die Fläche zwischen zwei Funktionen gezeichnet werden können. Dies ist mit dem Befehl einschluss möglich. Die Syntax ist die folgende:
einschluss
[layer=<  >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=<  >,<
>,<  >
>
[y=<  >,<
>,<  >]
>]
schnitt=<links|rechts|beide|keine>
<Funktionsterm  >,<Funktionsterm
>,<Funktionsterm  >
>
Ist der schnitt auf beide gesetzt, so werden automatisch die zwei Schnittpunkte einer Funktion berechnet. Analog wird bei links der linke Schnittpunkt berechnet und der rechte Zeichenbereich ist der  Wert.
Wert.
| einschluss-ptxt.ptxt |
|---|
| 1 achsen 2 einschluss layer=50 farbe=black,solid,red!20 linie=1,solid parameter="plotstyle=curve" x=-3,3 y=0,4 schnitt=beide (0.75*x)^4,(x)^2 3 graph x=-3,3 y=0,4 (0.75*x)^4 4 graph x=-3,3 y=0,4 (x)^2 |
6.7 Rotationskörper um die  -Achse
-Achse
Um einen Rotationskörper, der durch Rotation der Fläche, die durch den Graphen
der Funktion  im Intervall
im Intervall  , die
, die  -Achse und die
beiden Geraden
-Achse und die
beiden Geraden  und
und  begrenzt wird, um die
begrenzt wird, um die  -Achse
zu zeichnen, gibt es den Befehl graphrot
-Achse
zu zeichnen, gibt es den Befehl graphrot
graphrot
[layer=<  >]
>]
[farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=<  >,<
>,<  > [y=<
> [y=<  >,<
>,<  >]
>]
r=<Einteilung  >
>
<Funktionsterm  >
>
| graphrot-ptxt.ptxt |
|---|
| 1 groesse x=6 y=3 2 gitter 3 koordinatensystem x=0,6 y=-3,3 einteilung=1,1 skala=normal text="$x$","$y$" 4 graphrot farbe=black,shape,red!20 x=1,5 y=-3,3 r=4 2.5/(x^0.5) 5 |
| graphrot-2-ptxt.ptxt |
|---|
| 1 groesse x=6 y=3 2 gitter 3 koordinatensystem x=0,6 y=-3,3 einteilung=1,1 skala=normal text="$x$","$y$" 4 graphrot farbe=black,shape,red!20 x=1,5 y=-3,3 r=20 2.5/(x^0.5) 5 |
6.8 Parametrisierte Kurven
Unter einer Parameterdarstellung (auch Parametrisierung
oder Parametrierung) einer Kurve versteht man eine Darstellung,
bei der die Punkte der Kurve über einen einzigen Parameter abgelaufen
werden können. Ein Beispiel hierfür ist die Darstellung einer Schleife in der Form
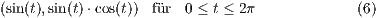
Die Syntax des Befehls ist die folgende:
parametricplot
[layer=<  >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
t=<  >,<
>,<  >
>
<Funktionsterm  >,<Funktionsterm
>,<Funktionsterm 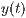 >
>
Wobei  das jeweilige Definitionsintervall beschreibt.
das jeweilige Definitionsintervall beschreibt.
| parametricplot-ptxt.ptxt |
|---|
| 1 koordinatensystem x=-2,2 y=-1,1 einteilung=1,1 linie=2,solid,black skala=normal text="$x$","$y$" 2 parametricplot layer=50 farbe=black linie=1,solid t=0,360 sin(t),sin(t)*cos(t) |
6.9 Zeichnen von Funktionsfolgen
Eine Funktionenfolge ist eine Folge  ,
,  von Funktionen
von Funktionen
 . Diese kann mit dem Befehl folge gezeichnet werden.
. Diese kann mit dem Befehl folge gezeichnet werden.
folge
[layer=<  >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
x=<  >,<
>,<  >
>
[r=<  >,<
>,<  >]
>]
<Funktionsterm  >
>
 gibt die Abstände der Punktfolgen an. Standardmäßig ist dies aus 1
gesetzt.
gibt die Abstände der Punktfolgen an. Standardmäßig ist dies aus 1
gesetzt.  definiert den Radius der Punkte und ist standardmäßig auf
definiert den Radius der Punkte und ist standardmäßig auf
 gesetzt.
gesetzt.
| folge-ptxt.ptxt |
|---|
| 1 achsen 2 folge layer=50 farbe=black linie=1,solid parameter="" x=-2,2 r=1,5 x^2 |
6.10 Plotten von Daten
Um Daten zu visualisieren gibt es in meinem Skript mehrere Befehle. Um dies zu veranschaulichen nutze ich im folgenden die Tabelle 6.10.
 in s in s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | 20 |
 in mA in mA | 130 | 100 | 80 | 70 | 55 | 45 | 40 | 30 | 25 | 20 | 7 | 3 |
Es gibt die drei Befehle listplot, fileplot und
dataplot. Diese realisieren die gleichnamigen Funktionen aus
Pstricks1. Die Syntax ist dabei bei
allen Funktionen die folgende:
[<fileplot|listplot|dataplot>]
[layer=<  >]
>]
[farbe=<Linienfarbe>]
[linie=<Linienstärke in pt (  )>,<Linienart>]
)>,<Linienart>]
[parameter="<Pstricksbefehle>"]
[lese <Dateiname>] oder <  >,<
>,<  > beliebig oft
> beliebig oft
ende
Es gibt mit dem Befehl lese die Möglichkeit eine Komma oder Semikol getrennte Datei einzulesen, oder direkt entsprechende Werte einzulesen.
| listplot-ptxt.ptxt |
|---|
| 1 groesse x=6 y=3 2 achsen 3 listplot farbe=red linie=1,solid parameter="showpoints=true" 4 1,130 5 2,100 6 3,80 7 4,70 8 5,55 9 6,45 10 7,40 11 8,30 12 9,25 13 10,20 14 15,7 15 20,3 16 ende 17 18 |
| fileplot-ptxt.ptxt |
|---|
| 1 groesse x=6 y=3 2 achsen 3 fileplot farbe=red linie=1,solid parameter="" 4 lese Abbildungen/kondensator-entladung.dat 5 ende 6 7 |
| dataplot-ptxt.ptxt |
|---|
| 1 groesse x=6 y=3 2 achsen 3 dataplot farbe=red linie=1,solid parameter="" 4 lese Abbildungen/kondensator-entladung.dat 5 ende 6 7 |
barplot
[layer=<
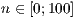 >]
>][farbe=<Linienfarbe>,<Füllart>,<Füllfarbe>]
[linie=<Linienstärke in pt (
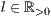 )>,<Linienart>]
)>,<Linienart>][parameter="<Pstricksbefehle>"]
[r=<Säulenbreite
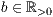 >]
>][lese <Dateiname>] oder <
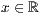 >,<
>,< 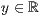 > beliebig oft
> beliebig oftende
| barplot-ptxt.ptxt |
|---|
| 1 groesse x=6 y=3 2 achsen 3 barplot farbe=red,solid,red!20 linie=1,solid r=0.5 4 lese Abbildungen/kondensator-entladung.dat 5 ende |
























