8 Mathematik und Physik
- Das mathematische Komma
- Integrale und Summen richtig setzen
- Neue Funktionen wie den arcsinh oder andere Funktionen setzen
- Zahlenmengen setzen
- Allgemeine Mengen setzen
- Eine Polynomdivision setzen
- Den Gauß-Algorithmus setzen
- Die Grundrechenarten
- Physikalische Einheiten richtig setzen
- Schaltskizzen erstellen
8.1 Das mathematische Komma
Damit im Mathemodus das Komma schöner aussieht, nutze ich das Paket ziffer1 von Martin Vaeth.
8.2 Integrale und Summen richtig setzen
Bei Integralen, Summen und noch so einigem mehr möchte ich die Grenzen direkt unter und über den jeweiligen Zeichen haben. Deshalb habe ich mir
| int-tex.tex |
|---|
| 1 \newcommand{\I}{\int\limits} 2 \newcommand{\Sum}{\sum\limits} 3 \newcommand{\Prod}{\prod\limits} |
Angewendet ergibt sich dann das folgende Integral oder Summenzeichen:
oder
bzw.
.
| int2-tex.tex |
|---|
| 1 $\I_a^b f(x) dx$ oder 2 $\Sum_{i=1}^n i$ bzw. 3 $\Prod_{i=1}^n i$ |
8.3 Neue Funktionen wie den arcsinh oder andere Funktionen setzen
Abkürzungen sind mal wieder alles in LATEX. Man muss nur darauf achten, dass man nicht zu viele hat und nachher wieder alles vergisst. Da ja der arcsinh o.ä. nicht kursiv im Mathemodus erscheinen sollen definiere ich mir die Funktionen wie folgt:
| arsin-tex.tex |
|---|
| 1 \newcommand{\arcsinh}{\operatorname{arcsinh}} |
8.4 Zahlenmengen setzen
Die natürlichen Zahlen 
, 
etc. Sollen natürlich schön mit dem Balken
vor dem Buchstaben angezeigt werden. Dafür ist es einfach sich Abkürzungen
| zahlen-tex.tex |
|---|
| 1 \newcommand{\N}{\ensuremath{\mathbb {N}}} 2 \newcommand{\Z}{\ensuremath{\mathbb {Z}}} 3 \newcommand{\Q}{\ensuremath{\mathbb {Q}}} 4 \newcommand{\R}{\ensuremath{\mathbb {R}}} 5 \newcommand{\C}{\ensuremath{\mathbb {C}}} |
8.5 Allgemeine Mengen setzen
Dazu habe ich mir ebenfalls Abkürzungen definiert, die ich später im
| menge-tex.tex |
|---|
| 1 \newcommand{\Mat}{\operatorname{Mat}} % Matrizen 2 \newcommand{\Vol}{\operatorname{Vol}} % Volumen |
8.6 Eine Polynomdivision setzen
Da LATEX ja sehr mächtig ist, muss man nicht mal selber eine Polynomdivision durchführen, sondern kann dies dem Paket polynom von Carsten Heinz und Hendri Adriaens überlassen2.
8.6.1 Beispiel
Eine einfache rationale Funktion:
Die Eingabe ist:
| polynom-tex.tex |
|---|
| 1 $\polylongdiv[style=C,div=:]{x^3-6x^2+11x-6}{x-2}$ |
8.7 Den Gauß-Algorithmus setzen
Um in der Oberstufe Lineare Gleichungssysteme zu lösen benötigt man das
Gauß-Verfahren. Meine erste Überlegung war mir ein eigenes Skript zu
erstellen, um dies ordentlich in LATEXzu setzen. Aber da hat sich bereits
Manuel Kauers Arbeit gemacht und das Paket gauss
geschrieben.3
Damit ist 
, 
und 
| gauss-verfahren-tex.tex |
|---|
| 1 $ \begin{gmatrix}[p] 2 -1 & 8 & 4 && 3,75 \\ 3 5 & 5 & 3 && 4 \\ 4 9 & -5 & 8 && 5 5 \rowops 6 \mult{0}{5}\add{0}{1} 7 \end{gmatrix} $ 8 9 $ \begin{gmatrix}[p] 10 -1 & 8 & 4 && 3,75 \\ 11 0 & 45 & 23 && 22,75 \\ 12 9 & -5 & 8 && 5 13 \rowops 14 \mult{0}{9}\add{0}{2} 15 \end{gmatrix}$ 16 17 $ \begin{gmatrix}[p] 18 -1 & 8 & 4 && 3,75 \\ 19 0 & 45 & 23 && 22,75 \\ 20 0 & 67 & 44 && 38,75 21 \rowops 22 \mult{2}{45} 23 \mult{1}{67}\add{1}{2} 24 \end{gmatrix}$ 25 26 $ \begin{gmatrix}[p] 27 -1 & 8 & 4 && 3,75 \\ 28 0 & 45 & 23 && 22,75 \\ 29 0 & 0 & 439 && 219,5 30 \end{gmatrix}$ 31 32 Damit ist $x_3 = 0,5 $, $x_2 = 0,25$ und $x_1 = 0,25$ |
8.8 Die Grundrechenarten
Als ich in Klasse 5 angefangen habe zu unterrichten habe ich mich auf die Suche gemacht, wie ich die Grundrechenarten in LATEXsetzen kann, ohne das alles per Hand machen zu müssen. Es gibt zwar das Paket xlop von Jean-Come Charpentier4. Da dies allerdings nicht ganz meinem Geschmack entsprach, habe ich ein Skript geschrieben, welches mir die Grundrechenarten setzt5.
8.8.1 Beispiel für die schriftliche Addition
Eine Beispielrechnung ist die folgende:
8.8.2 Beispiel für die schriftliche Subtraktion
Eine Beispielrechnung ist die folgende:
8.8.3 Beispiel für die schriftliche Multiplikation
Eine Beispielrechnung ist die folgende:
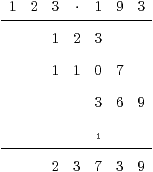
8.8.4 Die schriftliche Division
Im Folgenden wird nur die Division mit Rest behandelt. Ich führe hier einmal
ein Beispiel für den Algorithmus an:
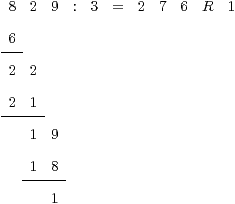
8.9 Physikalische Einheiten richtig setzen
Um auch die Einheiten im Mathemodus nicht kursiv zu setzen, nutze ich das
units-Paket von Axel Reichert6.
So kann man z.B. 
schön setzen:
| v-tex.tex |
|---|
| 1 $v = \unitfrac[1]{m}{s} = \unitfrac[3,6]{km}{h}$ |
\unit[...]{...}, um Einheiten ohne Bruch zu
setzen.
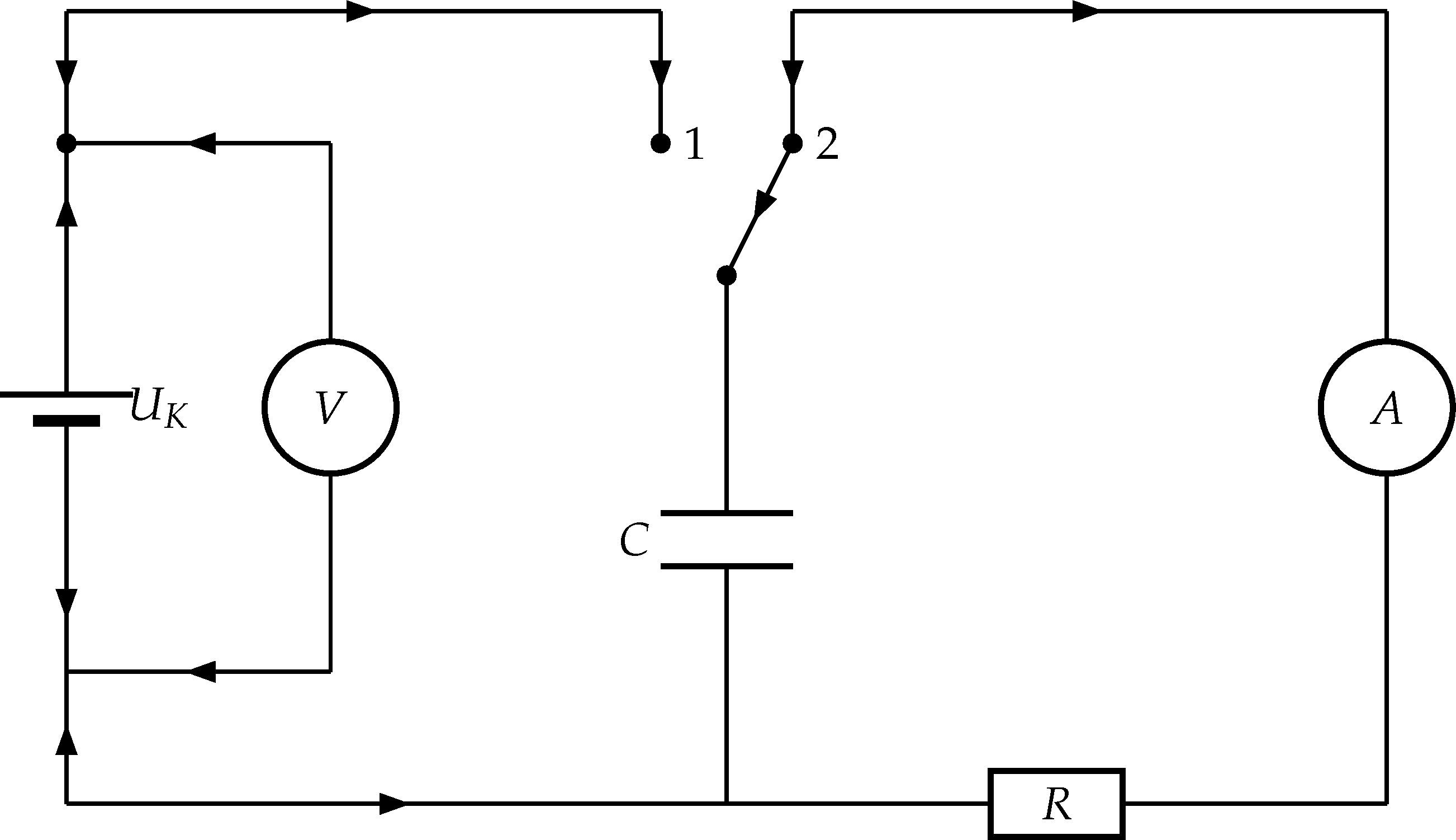
8.10 Schaltskizzen erstellen
Dazu gibt es für das Paket pstricks die Erweiterung pst-circ von Christophe Jorssen7. Dies ermöglicht es einem viele vorgefertigte Bauteile zu nutzen und diese einfach als Knoten zu verbinden. Ein Beispiel hierfür:
| entladung-tex.tex |
|---|
| 1 \begin{pspicture}(-2,-11)(12,1) 2 \pnode(0,0){A} \pnode(4.5,0){B} 3 \pnode(5.5,0){C} \pnode(10,0){D} 4 \pnode(0,-1){E} \pnode(4.5,-1){F} 5 \pnode(5.5,-1){G} \pnode(2,-5){P} 6 \uput[0](4.5,-1){1} 7 \uput[0](5.5,-1){2} 8 \pnode(0,-2){H} \pnode(5,-2){I} 9 \pnode(0,-4){J} \pnode(0,-5){K} 10 \pnode(0,-6){L} \pnode(5,-6){M} 11 \pnode(10,-6){N} \pnode(2,-1){O} 12 \wire(A)(B)\wire(C)(D)\wire(A)(E) 13 \wire(O)(E)\wire(H)(E)\wire(J)(K) 14 \wire(P)(K)\wire(L)(K)\wire(L)(M) 15 \wire(B)(F)\wire(C)(G)\wire(G)(I) 16 \wire(C)(D) 17 \pscircle*[fillstyle=solid](E){0.075} 18 \pscircle*[fillstyle=solid](I){0.075} 19 \pscircle*[fillstyle=solid](F){0.075} 20 \pscircle*[fillstyle=solid](G){0.075} 21 \resistor[labeloffset=0](M)(N){$R$} 22 \circledipole[labeloffset=0](N)(D){$A$} 23 \circledipole[labeloffset=0](O)(P){$V$} 24 \capacitor[](M)(I){$C$} 25 \battery(H)(J){$U_K$} 26 \end{pspicture} |
- 1
- Siehe [zif, 2009]
- 2
- Siehe [pol, 2009]
- 3
- Siehe [gau, 2009] und [Voß, 2009a, S. 191ff]
- 4
- Siehe [xlo, 2009]
- 5
- Siehe [Rendtel, 2009]
- 6
- Siehe [uni, 2009]
- 7
- Siehe [pst, 2009a]