Bewegung eines Satelliten
Öffnen Sie zunächst die nachfolgende Excel-Datei:
Zunächst einmal, zur Erklärung des Verfahrens:
Die Gravitationskraft 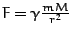 ist eine Zentralkraft, für die gilt
ist eine Zentralkraft, für die gilt 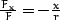 , also
, also
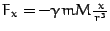 und genauso
und genauso 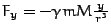 .
.
Um nun die Geschwindigkeit und die Positionen des Satellitens auf der Umlaufbahn zu bestimmen nutzt man das folgende Iterationsverfahren:
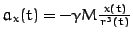 und
und
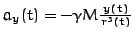 , wobei
, wobei
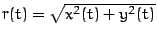 .
.
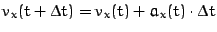 ,
,
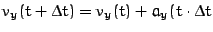 )
)
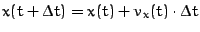 ,
,
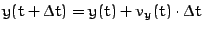
Beispiel
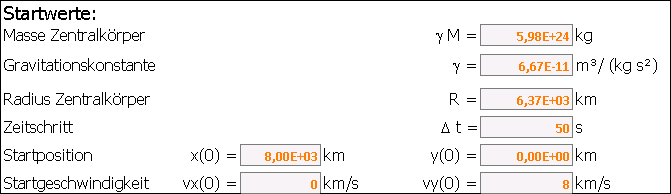
Wir starten mit den Werten 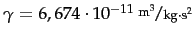 und der Masse der Erde
und der Masse der Erde 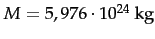 .
.
Die weiteren Werte sind 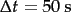 , sowie
, sowie
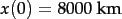 ,
,
![$y(0) = \unit[0]{km}$](gravimg16.png) und
und ![$v_x(0) =\unitfrac[0]{km}{s}$](gravimg17.png) ,
,
![$v_y(0) = \unitfrac[8]{km}{s}$](gravimg18.png)
Dann berechnen sich die Iterationsschritte wie folgt:
- erster Iterationsschritt:
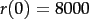 und
und
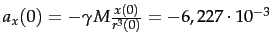 ,
,
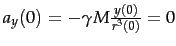 .
.
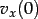 und
und 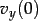 sind die Startwerte selbst.
sind die Startwerte selbst.
- zweiter Iterationsschritt:
-
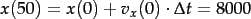 und
und
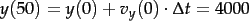 .
.
Damit kann
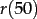 berechnet werden zu
berechnet werden zu
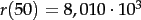 und damit
und damit
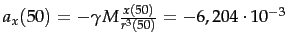 ,
,
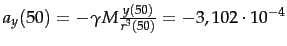 .
.
Hieraus lassen sich die Geschwindigkeiten bestimmen zu
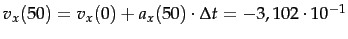 . Ebenso berechnet sich
. Ebenso berechnet sich 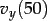 .
.
Aufgabe 1
Geben Sie folgende Startwerte ein:
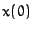 in km
in km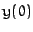 in km
in km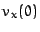 in km/s
in km/s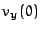 in km/s
in km/s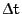 in s
in s8000 0 0 8 50 - Bestimmen Sie aus der Grafik näherungsweise die Geschwindigkeit im erdfernsten Punkt und vergleichen Sie diese mit der Geschwindigkeit im erdnächsten Punkt.
- Bestimmen Sie die große Halbachse der Ellipsenbahn. Tipp: Bestimmen Sie den Abstand des erdfernsten und erdnächsten Punktes und berechnen daraus die große Halbachse.
- Überprüfen Sie das 3. Keplersche Gesetz. Wählen Sie hierzu den Erdmond als Vergleichskörper. (Die Bahn des Erdmondes hat eine große Halbachse von ca. 3,82.105 km; seine Umlaufzeit beträgt 27,3 Tage.)
Aufgabe 2
- Der Startort befinde sich nun unmittelbar über der Erdoberfläche, die
Geschwindigkeit sei tangential zur Erdoberfläche orientiert. Wählen Sie also
z.B. für die Startwerte:
Der Betrag der Startgeschwindigkeit ist also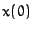 in km
in km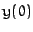 in km
in km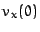 in km/s
in km/s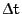 in s
in s6375 0 0 15 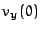 . Variieren Sie diesen Wert solange bis der Satellit gerade nach eine Kreisbahn um die Erde beschreibt.
. Variieren Sie diesen Wert solange bis der Satellit gerade nach eine Kreisbahn um die Erde beschreibt.
Diese Geschwindigkeit wird 1. kosmische Geschwindigkeit genannt. Vergleichen Sie diese mit dem Wert aus dem Buch.
- Der Satellit befinde sich nun 3632 km über der Erdoberfläche. Berechnen Sie die Geschwindigkeit, die erforderlich ist, dass er die Erde auf einer Kreisbahn umrundet. Überprüfen Sie diese Ergebnis mit der EXCEL-Anwendung. Wählen Sie z.B. folgende Startwerte:
Variieren Sie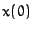 in km
in km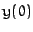 in km
in km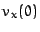 in km/s
in km/s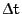 in s
in s10000 0 0 30 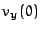 so lange, bis sich eine Kreisbahn ergibt, und vergleichen Sie die Geschwindigkeit mir dem Ergebnis von 1.
so lange, bis sich eine Kreisbahn ergibt, und vergleichen Sie die Geschwindigkeit mir dem Ergebnis von 1.
Letzte Änderung: 26.04.2012: 19:23:52 von X. Rendtel

Dieses Werk bzw. Inhalt steht unter einer Creative Commons Namensnennung-Weitergabe unter gleichen Bedingungen 3.0 Unported Lizenz.
Beruht auf einem Inhalt unter www.rendtel.de.