Skript zum Thema Interferenzhyperbeln

Diese Seite als pdf-Datei.

Inhaltsverzeichnis

Skript zum Thema Interferenzhyperbeln

1.1 Motivation

Im Physik Oberstufenkurs wird im ersten Semester das Thema Schwingungen und Wellen bearbeitet. Dort treten dann natürlich auch Interferenzhyperbeln auf. Nachdem ich dies nun schon mehrfach unterrichtet habe, habe ich mich privat mit der zugehörigen Mathematik beschäftigt. Hierzu gibt es einen netten Artikel bei der Wikipedia.¹
Herausgekommen ist ein kleines Perl-Skript, mitdem ich Kreise und Hyperbeln mithilfe von Pstricks erzeuge.

1.2 Die Theorie

Hat man zwei Erregerzentren von Wellen, so ergeben sich für die Interferenzmuster Hyperbelfunktionen. Eine Hyperbel ist definiert als die Menge aller Punkte der Zeichenebene, für die die Differenz der Abstände zu den Brennpunkten(erregerzentren) 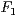und 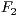konstant gleich 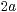ist, wobei die große Halbachse der Hyperbel ist.

Abb. 1: Eine Hyperbel

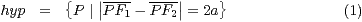
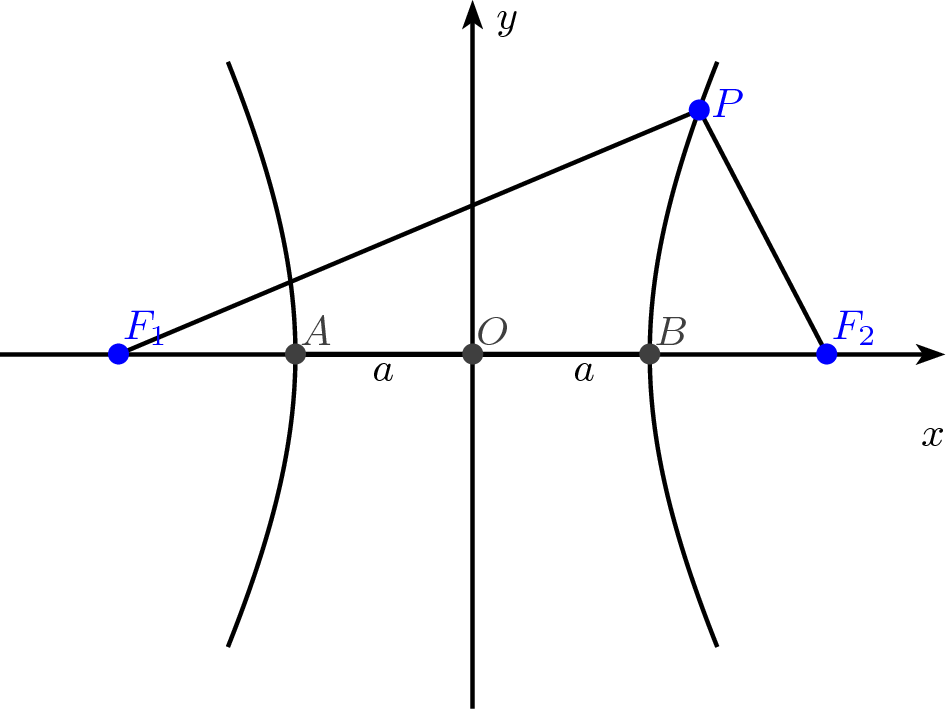
Den halben Abstand der Brennpunkte voneinander bezeichnet man üblicherweise mit . Die Gleichung der Hyperbel erhält eine besonders einfache Form, wenn sie in "‘1.Hauptlage"’ liegt, das heißt, dass die beiden Brennpunkte auf der 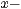Achse symmetrisch zum Ursprung liegen. Also in den Punkten 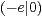und 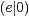. Es gilt dann für die Hyperbel

wobei gilt:

Hat man zwei Erreger mit der gleichen Wellenlänge, so liegen die Interferenzmaxima genau an den Stellen mit einem Gangunterschied von 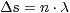, wobei 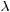die Wellenlänge ist und 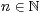. D. h man sucht einen Punkt 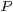auf der Interferenzhyperbel, der 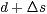vom linken Erreger und 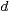vom rechten Erreger entfernt ist, für die rechte Verstärkung. Wobei oBdA 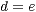ist. Es gilt dann: 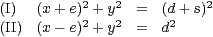Daraus ergibt sich: 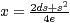und 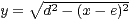Hieraus bestimmt man für die gesuchte Hyperbel :

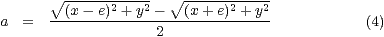
Setzt man dies nun in Gleichung (??) ein und löst dies nach 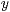auf, so hat man die Funktion für die Hyperbel.

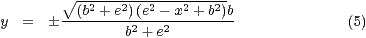
Mit einer geeigneten Parametrisierung erhält man:

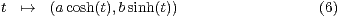
für .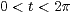

1.3 Programmeingabe

Wie erhält man nun die gewünschten Ergebnisse? Hierzu übergibt man an mein Skript eine Datei mit dem folgenden Eingabeformat:

abstand 3
wellenlaenge 1,2
gegen
boegen
hyperbel
anzahlkreise 1

Zur Erklärung: abstand n gibt an, wie weit die Erregerzentren auf der 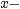Achse entfernt sind. wellenlaenge l1,l2 gibt die Wellenlängen der zwei Erreger an. Setzt man gegen, so wird startet der zweite Erreger gegenphasig zum ersten Erreger. Wird boegen gesetzt, so werden weitere Kreisbögen gezeichnet. anzahlkreise n gibt an, wie viele Kreise gezeichnet werden. Ist dies nicht gesetzt, so werden 4 Kreise gemalt.

1.3.1 Beispiele

Als Beispiel hier ein paar Eingaben für mein Programm und deren Ausgaben:

Die Eingabe:

abstand 3
wellenlaenge 1,1
boegen
hyperbel

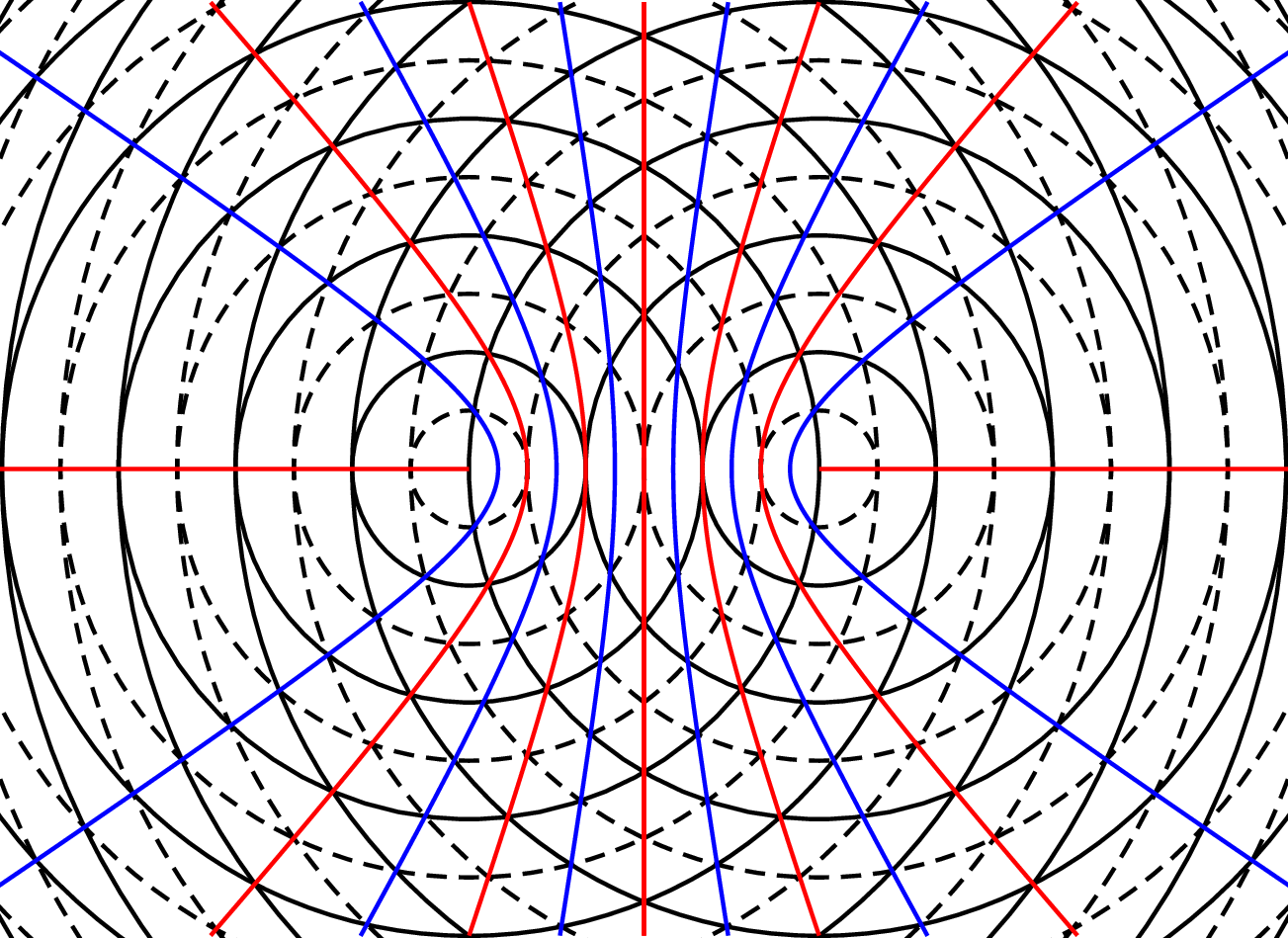Abb. 2: Ein erstes Bild

Die Eingabe:

abstand 3
wellenlaenge 1,2
gegen
boegen
hyperbel

Das Bild

Abb. 3: Ein zweites Bild

1.4 Programmcode

Und hier nun der vollständige Programmcode in Perl:

interferenz-pl.pl
1 #!/usr/bin/perl -w 2 ################################################################## 3 ## Programm zur Erstellung von Interferenzmustern mit Pstricks 4 ## Letzte Aenderung: 14.01.2010 5 ## Autor: Xenia Rendtel 6 ################################################################## 7 use POSIX qw /floor ceil/; 8 use Math::Trig; 9 use strict; 10 use lib '/home/xenia/Schule/Programme/Interferenz'; 11 use hilfsfunktionen; 12 my ( 13 $e, $s, $d, $l1, $l2, $weiter, 14 $kreise, $diff, $i, $ymax, $ymin, $xmin, 15 $xmax, @ausgabedatei, @ausgabedateizeilen, $kopf, $kommandodatei, $texdatei, 16 $leer, $eingabedateizeilen, @eingabedatei, $kommandodateinummer, $datei, 17 $zeile, $ausrichtung, $bezeichnung, $func, $variable, $j, 18 $schritt, 19 $spalten, $nachkommastellen, $spaltenausrichtung, $liste, $endeerreicht, 20 $hilfszeile, 21 $anzahlzeilen 22 ); 23 my $boegen = 0; 24 my $hyperbel = 0; 25 $xmin = $xmax = $ymin = $ymax = 0; 26 $kopf = 1; 27 $diff = 0; 28 ### Das Array wird eingelesen 29 @ausgabedateizeilen = (); 30 31 for ( $i = 0 ; $i <= 150 ; $i++ ) { $ausgabedateizeilen[$i] = 0; } 32 33 # In ein array wird geschrieben 34 sub schreibeinarray { 35 my ( $layer, $zeile ) = @_; 36 $ausgabedatei[$layer][ $ausgabedateizeilen[$layer] ] = $zeile; 37 $ausgabedateizeilen[$layer]++; 38 } 39 40 # Der Kopf der Latex-Datei wird geschrieben 41 sub kopfdatei { 42 if ( $kopf == 1 ) { 43 kommentar( 1, "Interferenzhyperbeln" ); 44 kommentar( 1, "Autor: X. Rendtel" ); 45 kommentar( 1, "Letzte Aenderung: 2009" ); 46 latex( 2, "\\documentclass[10pt, a4paper]{article}" ); 47 usepackage( "utf8", "inputenc" ); 48 usepackage( "", 49 "pstricks,pst-pdf,pst-node,xcolor, " 50 . "pst-circ,pst-func,pst-math,pst-eucl, " 51 . "pstricks-add,multido" ); 52 latex( 3, "\\pagestyle{empty} \n\\begin{document} " ); 53 } 54 beginpicture(4); 55 } 56 57 sub fussdatei { 58 endpicture(11); 59 if ( $kopf == 1 ) { latex( 11, "\\end{document}" ); } 60 } 61 #### Pictureumgebung 62 sub beginpicture { 63 my ($layer) = @_; 64 schreibeinarray( 65 $layer, 66 sprintf( 67 "\\begin{pspicture}(%g,%g)(%g,%g)\n", 68 getminmax( "x", "min" ), 69 getminmax( "y", "min" ), 70 getminmax( "x", "max" ), 71 getminmax( "y", "max" ) 72 ) 73 ); 74 } 75 76 sub endpicture { 77 my ($layer) = @_; 78 latex( $layer, "\\end{pspicture}" ); 79 } 80 81 # Die Eingabedatei wird gelesen 82 sub leseeingabedatei { 83 my $dateiname = shift(@_); 84 my $zeile; 85 open( my $EINGABEDATEI, $dateiname ) 86 \|\| die $dateiname . ": $!"; 87 while ( $zeile = <$EINGABEDATEI> ) { 88 89 # Zeilenenden beseitigen, Kommentare und Leerzeilen ignorieren 90 $zeile =~ s/[\r\n]//g; 91 $zeile =~ s/ +/ /g; 92 $zeile =~ s/ +$//g; 93 $zeile =~ s/^ +//g; 94 next if ( $zeile =~ /^\#/ ); 95 next if ( $zeile =~ /^$/ ); 96 if ( $zeile =~ /^lesedatei (.)$/i ) { 97 leseeingabedatei($1); 98 } 99 else { 100 $eingabedatei[$eingabedateizeilen] = $zeile; 101 $eingabedateizeilen++; 102 } 103 } 104 close($EINGABEDATEI); 105 } 106 ### Minimum und Maximum setzen 107 sub setminmax { 108 my ( $min, $xodery, $minmax ) = @_; 109 if ( $xodery eq "x" ) { 110 if ( $minmax eq "min" ) { $xmin = $min; } 111 else { $xmax = $min; } 112 } 113 if ( $xodery eq "y" ) { 114 if ( $minmax eq "min" ) { $ymin = $min; } 115 else { $ymax = $min; } 116 } 117 } 118 119 sub getminmax { 120 my ( $xodery, $minmax ) = @_; 121 if ( $xodery eq "x" ) { 122 if ( $minmax eq "min" ) { return $xmin; } 123 else { return $xmax; } 124 } 125 if ( $xodery eq "y" ) { 126 if ( $minmax eq "min" ) { return $ymin; } 127 else { return $ymax; } 128 } 129 } 130 ## Minimum und Maximum bestimmen 131 sub minmax { 132 my ( $xminlokal, $xmaxlokal, $yminlokal, $ymaxlokal ) = @_; 133 if ( $xminlokal < getminmax( "x", "min" ) ) { 134 setminmax( $xminlokal, "x", "min" ); 135 } 136 if ( $xmaxlokal > getminmax( "x", "max" ) ) { 137 setminmax( $xmaxlokal, "x", "max" ); 138 } 139 if ( $yminlokal < getminmax( "y", "min" ) ) { 140 setminmax( $yminlokal, "y", "min" ); 141 } 142 if ( $ymaxlokal > getminmax( "y", "max" ) ) { 143 setminmax( $ymaxlokal, "y", "max" ); 144 } 145 } 146 147 sub degtorad { 148 my ($wert) = @_; 149 return $wert pi() / 180; 150 } 151 152 sub radtodeg { 153 my ($wert) = @_; 154 return $wert * 180 / pi(); 155 } 156 my $abstand = 0; 157 158 sub setabstand { 159 my ($wert) = @_; 160 $abstand = $wert; 161 } 162 163 sub getabstand { return $abstand; } 164 165 my ( $wellenlaenge1, $wellenlaenge2 ); 166 $wellenlaenge1 = $wellenlaenge2 = 1; 167 168 sub setwelleeins { 169 my ($wert) = @_; 170 $wellenlaenge1 = $wert; 171 } 172 173 sub setwellezwei { 174 my ($wert) = @_; 175 $wellenlaenge2 = $wert; 176 } 177 178 sub getwelleeins { return $wellenlaenge1; } 179 180 sub getwellezwei { return $wellenlaenge2; } 181 my $anzahl = 4; 182 183 sub setkreisanzahl { 184 my ($wert) = @_; 185 $anzahl = $wert; 186 } 187 188 sub getkreisanzahl { return $anzahl; } 189 my $liniendicke = 1; 190 191 sub setliniendicke { 192 my ($wert) = @_; 193 $liniendicke = $wert; 194 } 195 196 sub getliniendicke { return $liniendicke; } 197 198 sub seterreger { 199 my ( $abstand, $wellenlaenge1, $wellenlaenge2, $anzahl, $liniendicke ) = @_; 200 $e = $abstand / 2; 201 kommentar( 2, "Abstand Erreger: " . $abstand ); 202 kommentar( 2, "Wellenlaenge Erreger 1: " . $wellenlaenge1 ); 203 kommentar( 2, "Wellenlaenge Erreger 2: " . $wellenlaenge2 ); 204 kommentar( 2, "Anzahl Kreise: " . $anzahl ); 205 ausgabe( 206 "\\psset{linecolor=black, fillcolor=black!20, " 207 . "linestyle=solid, linewidth= " 208 . $liniendicke 209 . "pt, dotstyle = , plotpoints = 1000, dotsize = 3pt," 210 . " arrowsize = 3pt 2, arrowinset = 0.25, xunit = 1cm, " 211 . "yunit = 1cm, algebraic =true} 212 " 213 ); 214 } 215 sub setboegen { my $wert = @_; $boegen = $wert; } 216 sub getboegen { return $boegen; } 217 ## Die Kreise werden gezeichnet 218 sub erzeugekreise { 219 my ( $x, $lambda, $start, $anzahlkreise ) = @_; 220 minmax( 221 $x - $lambda ($anzahlkreise), 222 $x + $lambda * ($anzahlkreise), 223 -$lambda * ($anzahlkreise), 224 $lambda * ($anzahlkreise) 225 ); 226 if ( getboegen() == 1 ) { $anzahlkreise = 5 * $anzahlkreise; } 227 else { $anzahlkreise = $anzahlkreise; } 228 if ( $start == 0 ) { 229 schreibeinarray( 10, 230 sprintf( "\\multido{\\nx=0+%f}{%i}{", $lambda, $anzahlkreise ) ); 231 schreibeinarray( 10, 232 sprintf( "\\pscircle[linewidth=1pt](%f,0){\\nx}}\n", $x ) ); 233 schreibeinarray( 234 10, 235 sprintf( 236 "\\multido{\\nx=%f+%f}{%i}{", 237 $lambda / 2, 238 $lambda, $anzahlkreise 239 ) 240 ); 241 schreibeinarray( 242 10, 243 sprintf( "\\pscircle[linestyle=dashed, linewidth=1pt](%f,0){\\nx}}\n", 244 $x ) 245 ); 246 } 247 else { 248 schreibeinarray( 10, 249 sprintf( "\\multido{\\nx=0+%f}{%i}{", $lambda, $anzahlkreise ) ); 250 schreibeinarray( 251 10, 252 sprintf( "\\pscircle[linestyle=dashed, linewidth=1pt](%f,0){\\nx}}\n", 253 $x ) 254 ); 255 schreibeinarray( 256 10, 257 sprintf( 258 "\\multido{\\nx=%f+%f}{%i}{", 259 $lambda / 2, 260 $lambda, $anzahlkreise 261 ) 262 ); 263 schreibeinarray( 10, 264 sprintf( "\\pscircle[linewidth=1pt](%f,0){\\nx}}\n", $x ) ); 265 } 266 } 267 268 sub hyperbelfunktion { 269 my ( $a, $e, $ymin, $ymax, $farbe ) = @_; 270 my $b = sqrt( $e * $e - $a * $a ); 271 my $i = 0; 272 my $t = 0; 273 for ( $i = 0 ; $i <= 3 ; $i = $i + 1 / 1000 ) { 274 if ( $b * sinh($i) < $ymax ) { $t = $i; } 275 else { $t = $t; } 276 } 277 schreibeinarray( 278 10, 279 sprintf( 280 "\\parametricplot[linecolor=%s]{%g}{%g}{%gCOSH(t)\|%gSINH(t)}", 281 $farbe, -$t, $t, $a, $b 282 ) 283 ); 284 schreibeinarray( 285 10, 286 sprintf( 287 "\\parametricplot[linecolor=%s]{%g}{%g}{%gCOSH(t)\|%gSINH(t)}", 288 $farbe, -$t, $t, -$a, -$b 289 ) 290 ); 291 } 292 293 sub kreisboegen { 294 my ( $x1, $laenge, $kreise, $start ) = @_; 295 my ( $xabstandlinks, $xabstandrechts, $alpha, $beta, $gamma, $delta, $i, 296 $abstand, $eckelinks, $eckerechts, $berg, $tal, ); 297 if ( $start == 0 ) { $berg = "solid"; $tal = "dashed"; } 298 else { $berg = "dashed"; $tal = "solid"; } 299 } 300 301 sub kreisboegen2 { 302 my ( $x1, $laenge, $kreise, $start ) = @_; 303 my ( $xabstandlinks, $xabstandrechts, $alpha, $beta, $gamma, $delta, $i, 304 $abstand, $eckelinks, $eckerechts, $berg, $tal, ); 305 if ( $start == 0 ) { $berg = "solid"; $tal = "dashed"; } 306 else { $berg = "dashed"; $tal = "solid"; } 307 $xabstandlinks = abs( $x1 - $xmin ); 308 $xabstandrechts = abs( $xmax - $x1 ); 309 $eckelinks = sqrt( $ymax * $ymax + $xabstandlinks * $xabstandlinks ); 310 $eckerechts = sqrt( $ymax * $ymax + $xabstandrechts * $xabstandrechts ); 311 312 for ( $i = 0 ; $i <= 100 ; $i++ ) { 313 $abstand = ( $kreise * $laenge ) + $laenge * $i; 314 if ( $abstand <= $xabstandlinks ) { 315 $beta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 ); 316 if ( $abstand <= $eckelinks ) { 317 schreibeinarray( 318 10, 319 sprintf( 320 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 321 $berg, $x1, $abstand, 90 + $beta, 270 - $beta 322 ) 323 ); 324 } 325 } 326 else { 327 $alpha = 328 nachkommastellen( radtodeg( acos( $xabstandlinks / $abstand ) ), 4 ); 329 $beta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 ); 330 if ( $abstand <= $eckelinks ) { 331 schreibeinarray( 332 10, 333 sprintf( 334 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 335 $berg, $x1, $abstand, 90 + $beta, 180 - $alpha 336 ) 337 ); 338 schreibeinarray( 339 10, 340 sprintf( 341 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 342 $berg, $x1, $abstand, 343 180 + $alpha, 344 270 - $beta 345 ) 346 ); 347 } 348 } 349 if ( $abstand <= $xabstandrechts ) { 350 $delta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 ); 351 if ( $abstand <= $eckerechts ) { 352 schreibeinarray( 353 10, 354 sprintf( 355 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 356 $berg, $x1, $abstand, 357 270 + $delta, 358 90 - $delta 359 ) 360 ); 361 } 362 } 363 else { 364 $gamma = 365 nachkommastellen( radtodeg( acos( $xabstandrechts / $abstand ) ), 4 ); 366 $delta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 ); 367 if ( $abstand <= $eckerechts ) { 368 schreibeinarray( 369 10, 370 sprintf( 371 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 372 $berg, $x1, $abstand, $gamma, 90 - $delta 373 ) 374 ); 375 schreibeinarray( 376 10, 377 sprintf( 378 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 379 $berg, $x1, $abstand, 380 270 + $delta, 381 360 - $gamma 382 ) 383 ); 384 } 385 } 386 } 387 for ( $i = 0 ; $i <= 100 ; $i++ ) { 388 $abstand = ( $kreise * $laenge + $laenge / 2 ) + $laenge * $i; 389 if ( $abstand <= $xabstandlinks ) { 390 $beta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 ); 391 if ( $abstand <= $eckelinks ) { 392 schreibeinarray( 393 10, 394 sprintf( 395 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 396 $tal, $x1, $abstand, 90 + $beta, 270 - $beta 397 ) 398 ); 399 } 400 } 401 else { 402 $alpha = 403 nachkommastellen( radtodeg( acos( $xabstandlinks / $abstand ) ), 4 ); 404 $beta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 ); 405 if ( $abstand <= $eckelinks ) { 406 schreibeinarray( 407 10, 408 sprintf( 409 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 410 $tal, $x1, $abstand, 90 + $beta, 180 - $alpha 411 ) 412 ); 413 schreibeinarray( 414 10, 415 sprintf( 416 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 417 $tal, $x1, $abstand, 418 180 + $alpha, 419 270 - $beta 420 ) 421 ); 422 } 423 } 424 if ( $abstand <= $xabstandrechts ) { 425 $delta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 ); 426 if ( $abstand <= $eckerechts ) { 427 schreibeinarray( 428 10, 429 sprintf( 430 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 431 $tal, $x1, $abstand, 432 270 + $delta, 433 90 - $delta 434 ) 435 ); 436 } 437 } 438 else { 439 $gamma = radtodeg( acos( $xabstandrechts / $abstand ) ); 440 $delta = radtodeg( acos( $ymax / $abstand ) ); 441 if ( $abstand <= $eckerechts ) { 442 schreibeinarray( 443 10, 444 sprintf( 445 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 446 $tal, $x1, $abstand, $gamma, 90 - $delta 447 ) 448 ); 449 schreibeinarray( 450 10, 451 sprintf( 452 "\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}", 453 $tal, $x1, $abstand, 454 270 + $delta, 455 360 - $gamma 456 ) 457 ); 458 } 459 } 460 } 461 ausgabe(""); 462 } 463 464 sub hyperbel { 465 my ( $e, $laenge1, $laenge2, $anzahl ) = @_; 466 my ( $a, $s, $d, $n, $x, $y, $xhilf, $yhilf, $xnext, $ynext, $genau ); 467 $genau = 0; 468 $d = ceil($e); 469 for ( $n = 0 ; $n <= $anzahl ; $n++ ) { 470 $s = $laenge1 * $n; 471 $xhilf = nachkommastellen( ( 2 * $d * $s + $s * $s ) / ( 4 * $e ), 4 ); 472 if ( ( $d * $d - ( $xhilf - $e ) * ( $xhilf - $e ) ) >= 0 ) { 473 $yhilf = 474 nachkommastellen( sqrt( $d * $d - ( $xhilf - $e ) * ( $xhilf - $e ) ), 475 4 ); 476 $a = ( 477 sqrt( ( $xhilf - $e ) * ( $xhilf - $e ) + $yhilf * $yhilf ) - 478 sqrt( ( $xhilf + $e ) * ( $xhilf + $e ) + $yhilf * $yhilf ) ) / 2; 479 if ( $diff == 1 ) { 480 hyperbelfunktion( $a, $e, -$ymax, $ymax, "blue" ); 481 } 482 else { 483 hyperbelfunktion( $a, $e, -$ymax, $ymax, "red" ); 484 } 485 } 486 } 487 for ( $n = 1 ; $n <= $anzahl ; $n++ ) { 488 $s = ( 2 * $n - 1 ) * $laenge1 / 2; 489 $xhilf = ( 2 * $d * $s + $s * $s ) / ( 4 * $e ); 490 if ( ( $d * $d - ( $xhilf - $e ) * ( $xhilf - $e ) ) >= 0 ) { 491 $yhilf = sqrt( $d * $d - ( $xhilf - $e ) * ( $xhilf - $e ) ); 492 $a = ( 493 sqrt( ( $xhilf - $e ) * ( $xhilf - $e ) + $yhilf * $yhilf ) - 494 sqrt( ( $xhilf + $e ) * ( $xhilf + $e ) + $yhilf * $yhilf ) ) / 2; 495 if ( $diff == 1 ) { 496 hyperbelfunktion( $a, $e, -$ymax, $ymax, "red" ); 497 } 498 else { 499 hyperbelufnktion( $a, $e, -$ymax, $ymax, "blue" ); 500 } 501 } 502 } 503 } 504 my $start1 = 0; 505 my $start2 = 0; 506 $kommandodateinummer = 0; 507 while ( exists $ARGV[$kommandodateinummer] ) { 508 $kommandodatei = $ARGV[$kommandodateinummer]; 509 $texdatei = $kommandodatei; 510 $texdatei =~ s/\.ptxt$//i; 511 $texdatei = $texdatei . " . adam "; 512 $kommandodateinummer++; 513 $eingabedateizeilen = 0; 514 leseeingabedatei($kommandodatei); 515 for ( $i = 0 ; $i < $eingabedateizeilen ; $i++ ) { 516 $zeile = $eingabedatei[$i]; 517 if ( $zeile =~ /^abstand( [-0-9\.]+)$/i ) { 518 setabstand($1); 519 } 520 elsif ( $zeile =~ /^anzahlkreise( [-0-9\.]+)$/i ) { 521 setkreisanzahl($1); 522 } 523 elsif ( $zeile =~ /^wellenlaenge( [-0-9\.]+),([-0-9\.]+)$/i ) { 524 setwelleeins($1); 525 setwellezwei($2); 526 } 527 elsif ( $zeile =~ /^gegen$/i ) { $start2 = 1; $diff = 1; } 528 elsif ( $zeile =~ /^boegen$/i ) { setboegen(1); } 529 elsif ( $zeile =~ /^hyperbel$/i ) { $hyperbel = 1; } 530 531 # Alle anderen Befehle sind Schrott 532 else { printf( "%% Unbekannter Befehl '%s'\n", $zeile ); } 533 } 534 } 535 seterreger( 536 getabstand(), getwelleeins(), getwellezwei(), getkreisanzahl(), 537 getliniendicke() 538 ); 539 erzeugekreise( -$e, getwelleeins(), $start1, getkreisanzahl() ); 540 erzeugekreise( $e, getwellezwei(), $start2, getkreisanzahl() ); 541 if ( $hyperbel == 1 ) { 542 hyperbel( $e, getwelleeins(), getwellezwei(), 1000 ); 543 } 544 $leer = 1; 545 my $layer; 546 for ( $layer = 0 ; $layer <= 100 ; $layer++ ) { 547 548 for ( $i = 0 ; $i < $ausgabedateizeilen[$layer] ; $i++ ) { 549 $leer = 0; 550 } 551 } 552 if ( $leer == 0 ) { 553 kopfdatei(); 554 fussdatei(); 555 for ( $layer = 0 ; $layer <= 11 ; $layer++ ) { 556 for ( $i = 0 ; $i < $ausgabedateizeilen[$layer] ; $i++ ) { 557 printf( "%s \n", $ausgabedatei[$layer][$i] ); 558 } 559 } 560 } 561 else { printf("%% Die Datei ist leer \n"); } 562

interferenz-pl.pl

#!/usr/bin/perl -w
##################################################################
## Programm zur Erstellung von Interferenzmustern mit Pstricks
## Letzte Aenderung: 14.01.2010
## Autor: Xenia Rendtel
##################################################################
use POSIX qw /floor ceil/;
use Math::Trig;
use strict;
use lib '/home/xenia/Schule/Programme/Interferenz';
use hilfsfunktionen;
my (
$e, $s, $d, $l1, $l2, $weiter,
$kreise, $diff, $i, $ymax, $ymin, $xmin,
$xmax, @ausgabedatei, @ausgabedateizeilen, $kopf, $kommandodatei, $texdatei,
$leer, $eingabedateizeilen, @eingabedatei, $kommandodateinummer, $datei,
$zeile, $ausrichtung, $bezeichnung, $func, $variable, $j,
$schritt,
$spalten, $nachkommastellen, $spaltenausrichtung, $liste, $endeerreicht,
$hilfszeile,
$anzahlzeilen
);
my $boegen = 0;
my $hyperbel = 0;
$xmin = $xmax = $ymin = $ymax = 0;
$kopf = 1;
$diff = 0;
### Das Array wird eingelesen
@ausgabedateizeilen = ();

for ( $i = 0 ; $i <= 150 ; $i++ ) { $ausgabedateizeilen[$i] = 0; }

# In ein array wird geschrieben
sub schreibeinarray {
my ( $layer, $zeile ) = @_;
$ausgabedatei[$layer][ $ausgabedateizeilen[$layer] ] = $zeile;
$ausgabedateizeilen[$layer]++;
}

# Der Kopf der Latex-Datei wird geschrieben
sub kopfdatei {
if ( $kopf == 1 ) {
	kommentar( 1, "Interferenzhyperbeln" );
	kommentar( 1, "Autor: X. Rendtel" );
	kommentar( 1, "Letzte Aenderung: 2009" );
	latex( 2, "\\documentclass[10pt, a4paper]{article}" );
	usepackage( "utf8", "inputenc" );
	usepackage( "",
		 "pstricks,pst-pdf,pst-node,xcolor, "
			. "pst-circ,pst-func,pst-math,pst-eucl, "
			. "pstricks-add,multido" );
	latex( 3, "\\pagestyle{empty} \n\\begin{document} " );
}
beginpicture(4);
}

sub fussdatei {
endpicture(11);
if ( $kopf == 1 ) { latex( 11, "\\end{document}" ); }
}
#### Pictureumgebung
sub beginpicture {
my ($layer) = @_;
schreibeinarray(
	$layer,
	sprintf(
		"\\begin{pspicture}(%g,%g)(%g,%g)\n",
		getminmax( "x", "min" ),
		getminmax( "y", "min" ),
		getminmax( "x", "max" ),
		getminmax( "y", "max" )
	)
);
}

sub endpicture {
my ($layer) = @_;
latex( $layer, "\\end{pspicture}" );
}

# Die Eingabedatei wird gelesen
sub leseeingabedatei {
my $dateiname = shift(@_);
my $zeile;
open( my $EINGABEDATEI, $dateiname )
	|| die $dateiname . ": $!";
while ( $zeile = <$EINGABEDATEI> ) {

	# Zeilenenden beseitigen, Kommentare und Leerzeilen ignorieren
	$zeile =~ s/[\r\n]//g;
	$zeile =~ s/ +/ /g;
	$zeile =~ s/ +$//g;
	$zeile =~ s/^ +//g;
	next if ( $zeile =~ /^\#/ );
	next if ( $zeile =~ /^$/ );
	if ( $zeile =~ /^lesedatei (.*)$/i ) {
		leseeingabedatei($1);
	}
	else {
		$eingabedatei[$eingabedateizeilen] = $zeile;
		$eingabedateizeilen++;
	}
}
close($EINGABEDATEI);
}
### Minimum und Maximum setzen
sub setminmax {
my ( $min, $xodery, $minmax ) = @_;
if ( $xodery eq "x" ) {
	if ( $minmax eq "min" ) { $xmin = $min; }
	else { $xmax = $min; }
}
if ( $xodery eq "y" ) {
	if ( $minmax eq "min" ) { $ymin = $min; }
	else { $ymax = $min; }
}
}

sub getminmax {
my ( $xodery, $minmax ) = @_;
if ( $xodery eq "x" ) {
	if ( $minmax eq "min" ) { return $xmin; }
	else { return $xmax; }
}
if ( $xodery eq "y" ) {
	if ( $minmax eq "min" ) { return $ymin; }
	else { return $ymax; }
}
}
## Minimum und Maximum bestimmen
sub minmax {
my ( $xminlokal, $xmaxlokal, $yminlokal, $ymaxlokal ) = @_;
if ( $xminlokal < getminmax( "x", "min" ) ) {
	setminmax( $xminlokal, "x", "min" );
}
if ( $xmaxlokal > getminmax( "x", "max" ) ) {
	setminmax( $xmaxlokal, "x", "max" );
}
if ( $yminlokal < getminmax( "y", "min" ) ) {
	setminmax( $yminlokal, "y", "min" );
}
if ( $ymaxlokal > getminmax( "y", "max" ) ) {
	setminmax( $ymaxlokal, "y", "max" );
}
}

sub degtorad {
my ($wert) = @_;
return $wert * pi() / 180;
}

sub radtodeg {
my ($wert) = @_;
return $wert * 180 / pi();
}
my $abstand = 0;

sub setabstand {
my ($wert) = @_;
$abstand = $wert;
}

sub getabstand { return $abstand; }

my ( $wellenlaenge1, $wellenlaenge2 );
$wellenlaenge1 = $wellenlaenge2 = 1;

sub setwelleeins {
my ($wert) = @_;
$wellenlaenge1 = $wert;
}

sub setwellezwei {
my ($wert) = @_;
$wellenlaenge2 = $wert;
}

sub getwelleeins { return $wellenlaenge1; }

sub getwellezwei { return $wellenlaenge2; }
my $anzahl = 4;

sub setkreisanzahl {
my ($wert) = @_;
$anzahl = $wert;
}

sub getkreisanzahl { return $anzahl; }
my $liniendicke = 1;

sub setliniendicke {
my ($wert) = @_;
$liniendicke = $wert;
}

sub getliniendicke { return $liniendicke; }

sub seterreger {
my ( $abstand, $wellenlaenge1, $wellenlaenge2, $anzahl, $liniendicke ) = @_;
$e = $abstand / 2;
kommentar( 2, "Abstand Erreger: " . $abstand );
kommentar( 2, "Wellenlaenge Erreger 1: " . $wellenlaenge1 );
kommentar( 2, "Wellenlaenge Erreger 2: " . $wellenlaenge2 );
kommentar( 2, "Anzahl Kreise: " . $anzahl );
ausgabe(
	 "\\psset{linecolor=black, fillcolor=black!20, "
		. "linestyle=solid, linewidth= "
		. $liniendicke
		. "pt, dotstyle = *, plotpoints = 1000, dotsize = 3pt,"
		. " arrowsize = 3pt 2, arrowinset = 0.25, xunit = 1cm, "
		. "yunit = 1cm, algebraic =true}
"
);
}
sub setboegen { my $wert = @_; $boegen = $wert; }
sub getboegen { return $boegen; }
## Die Kreise werden gezeichnet
sub erzeugekreise {
my ( $x, $lambda, $start, $anzahlkreise ) = @_;
minmax(
	$x - $lambda * ($anzahlkreise),
	$x + $lambda * ($anzahlkreise),
	-$lambda * ($anzahlkreise),
	$lambda * ($anzahlkreise)
);
if ( getboegen() == 1 ) { $anzahlkreise = 5 * $anzahlkreise; }
else { $anzahlkreise = $anzahlkreise; }
if ( $start == 0 ) {
	schreibeinarray( 10,
		sprintf( "\\multido{\\nx=0+%f}{%i}{", $lambda, $anzahlkreise ) );
	schreibeinarray( 10,
		sprintf( "\\pscircle[linewidth=1pt](%f,0){\\nx}}\n", $x ) );
	schreibeinarray(
		10,
		sprintf(
			"\\multido{\\nx=%f+%f}{%i}{",
			$lambda / 2,
			$lambda, $anzahlkreise
		)
	);
	schreibeinarray(
		10,
		sprintf( "\\pscircle[linestyle=dashed, linewidth=1pt](%f,0){\\nx}}\n",
			$x )
	);
}
else {
	schreibeinarray( 10,
		sprintf( "\\multido{\\nx=0+%f}{%i}{", $lambda, $anzahlkreise ) );
	schreibeinarray(
		10,
		sprintf( "\\pscircle[linestyle=dashed, linewidth=1pt](%f,0){\\nx}}\n",
			$x )
	);
	schreibeinarray(
		10,
		sprintf(
			"\\multido{\\nx=%f+%f}{%i}{",
			$lambda / 2,
			$lambda, $anzahlkreise
		)
	);
	schreibeinarray( 10,
		sprintf( "\\pscircle[linewidth=1pt](%f,0){\\nx}}\n", $x ) );
}
}

sub hyperbelfunktion {
my ( $a, $e, $ymin, $ymax, $farbe ) = @_;
my $b = sqrt( $e * $e - $a * $a );
my $i = 0;
my $t = 0;
for ( $i = 0 ; $i <= 3 ; $i = $i + 1 / 1000 ) {
	if ( $b * sinh($i) < $ymax ) { $t = $i; }
	else { $t = $t; }
}
schreibeinarray(
	10,
	sprintf(
		"\\parametricplot[linecolor=%s]{%g}{%g}{%g*COSH(t)|%g*SINH(t)}",
		$farbe, -$t, $t, $a, $b
	)
);
schreibeinarray(
	10,
	sprintf(
		"\\parametricplot[linecolor=%s]{%g}{%g}{%g*COSH(t)|%g*SINH(t)}",
		$farbe, -$t, $t, -$a, -$b
	)
);
}

sub kreisboegen {
my ( $x1, $laenge, $kreise, $start ) = @_;
my ( $xabstandlinks, $xabstandrechts, $alpha, $beta, $gamma, $delta, $i,
	$abstand, $eckelinks, $eckerechts, $berg, $tal, );
if ( $start == 0 ) { $berg = "solid"; $tal = "dashed"; }
else { $berg = "dashed"; $tal = "solid"; }
}

sub kreisboegen2 {
my ( $x1, $laenge, $kreise, $start ) = @_;
my ( $xabstandlinks, $xabstandrechts, $alpha, $beta, $gamma, $delta, $i,
	$abstand, $eckelinks, $eckerechts, $berg, $tal, );
if ( $start == 0 ) { $berg = "solid"; $tal = "dashed"; }
else { $berg = "dashed"; $tal = "solid"; }
$xabstandlinks = abs( $x1 - $xmin );
$xabstandrechts = abs( $xmax - $x1 );
$eckelinks = sqrt( $ymax * $ymax + $xabstandlinks * $xabstandlinks );
$eckerechts = sqrt( $ymax * $ymax + $xabstandrechts * $xabstandrechts );

for ( $i = 0 ; $i <= 100 ; $i++ ) {
	$abstand = ( $kreise * $laenge ) + $laenge * $i;
	if ( $abstand <= $xabstandlinks ) {
		$beta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 );
		if ( $abstand <= $eckelinks ) {
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$berg, $x1, $abstand, 90 + $beta, 270 - $beta
				)
			);
		}
	}
	else {
		$alpha =
			nachkommastellen( radtodeg( acos( $xabstandlinks / $abstand ) ), 4 );
		$beta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 );
		if ( $abstand <= $eckelinks ) {
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$berg, $x1, $abstand, 90 + $beta, 180 - $alpha
				)
			);
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$berg, $x1, $abstand,
					180 + $alpha,
					270 - $beta
				)
			);
		}
	}
	if ( $abstand <= $xabstandrechts ) {
		$delta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 );
		if ( $abstand <= $eckerechts ) {
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$berg, $x1, $abstand,
					270 + $delta,
					90 - $delta
				)
			);
		}
	}
	else {
		$gamma =
			nachkommastellen( radtodeg( acos( $xabstandrechts / $abstand ) ), 4 );
		$delta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 );
		if ( $abstand <= $eckerechts ) {
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$berg, $x1, $abstand, $gamma, 90 - $delta
				)
			);
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$berg, $x1, $abstand,
					270 + $delta,
					360 - $gamma
				)
			);
		}
	}
}
for ( $i = 0 ; $i <= 100 ; $i++ ) {
	$abstand = ( $kreise * $laenge + $laenge / 2 ) + $laenge * $i;
	if ( $abstand <= $xabstandlinks ) {
		$beta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 );
		if ( $abstand <= $eckelinks ) {
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$tal, $x1, $abstand, 90 + $beta, 270 - $beta
				)
			);
		}
	}
	else {
		$alpha =
			nachkommastellen( radtodeg( acos( $xabstandlinks / $abstand ) ), 4 );
		$beta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 );
		if ( $abstand <= $eckelinks ) {
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$tal, $x1, $abstand, 90 + $beta, 180 - $alpha
				)
			);
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$tal, $x1, $abstand,
					180 + $alpha,
					270 - $beta
				)
			);
		}
	}
	if ( $abstand <= $xabstandrechts ) {
		$delta = nachkommastellen( radtodeg( acos( $ymax / $abstand ) ), 4 );
		if ( $abstand <= $eckerechts ) {
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$tal, $x1, $abstand,
					270 + $delta,
					90 - $delta
				)
			);
		}
	}
	else {
		$gamma = radtodeg( acos( $xabstandrechts / $abstand ) );
		$delta = radtodeg( acos( $ymax / $abstand ) );
		if ( $abstand <= $eckerechts ) {
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$tal, $x1, $abstand, $gamma, 90 - $delta
				)
			);
			schreibeinarray(
				10,
				sprintf(
					"\\psarc[linestyle=%s](%g,0){%g}{%g}{%g}",
					$tal, $x1, $abstand,
					270 + $delta,
					360 - $gamma
				)
			);
		}
	}
}
ausgabe("");
}

sub hyperbel {
my ( $e, $laenge1, $laenge2, $anzahl ) = @_;
my ( $a, $s, $d, $n, $x, $y, $xhilf, $yhilf, $xnext, $ynext, $genau );
$genau = 0;
$d = ceil($e);
for ( $n = 0 ; $n <= $anzahl ; $n++ ) {
	$s = $laenge1 * $n;
	$xhilf = nachkommastellen( ( 2 * $d * $s + $s * $s ) / ( 4 * $e ), 4 );
	if ( ( $d * $d - ( $xhilf - $e ) * ( $xhilf - $e ) ) >= 0 ) {
		$yhilf =
			nachkommastellen( sqrt( $d * $d - ( $xhilf - $e ) * ( $xhilf - $e ) ),
			4 );
		$a = (
			sqrt( ( $xhilf - $e ) * ( $xhilf - $e ) + $yhilf * $yhilf ) -
				sqrt( ( $xhilf + $e ) * ( $xhilf + $e ) + $yhilf * $yhilf ) ) / 2;
		if ( $diff == 1 ) {
			hyperbelfunktion( $a, $e, -$ymax, $ymax, "blue" );
		}
		else {
			hyperbelfunktion( $a, $e, -$ymax, $ymax, "red" );
		}
	}
}
for ( $n = 1 ; $n <= $anzahl ; $n++ ) {
	$s = ( 2 * $n - 1 ) * $laenge1 / 2;
	$xhilf = ( 2 * $d * $s + $s * $s ) / ( 4 * $e );
	if ( ( $d * $d - ( $xhilf - $e ) * ( $xhilf - $e ) ) >= 0 ) {
		$yhilf = sqrt( $d * $d - ( $xhilf - $e ) * ( $xhilf - $e ) );
		$a = (
			sqrt( ( $xhilf - $e ) * ( $xhilf - $e ) + $yhilf * $yhilf ) -
				sqrt( ( $xhilf + $e ) * ( $xhilf + $e ) + $yhilf * $yhilf ) ) / 2;
		if ( $diff == 1 ) {
			hyperbelfunktion( $a, $e, -$ymax, $ymax, "red" );
		}
		else {
			hyperbelufnktion( $a, $e, -$ymax, $ymax, "blue" );
		}
	}
}
}
my $start1 = 0;
my $start2 = 0;
$kommandodateinummer = 0;
while ( exists $ARGV[$kommandodateinummer] ) {
$kommandodatei = $ARGV[$kommandodateinummer];
$texdatei = $kommandodatei;
$texdatei =~ s/\.ptxt$//i;
$texdatei = $texdatei . " . adam ";
$kommandodateinummer++;
$eingabedateizeilen = 0;
leseeingabedatei($kommandodatei);
for ( $i = 0 ; $i < $eingabedateizeilen ; $i++ ) {
	$zeile = $eingabedatei[$i];
	if ( $zeile =~ /^abstand( [-0-9\.]+)$/i ) {
		setabstand($1);
	}
	elsif ( $zeile =~ /^anzahlkreise( [-0-9\.]+)$/i ) {
		setkreisanzahl($1);
	}
	elsif ( $zeile =~ /^wellenlaenge( [-0-9\.]+),([-0-9\.]+)$/i ) {
		setwelleeins($1);
		setwellezwei($2);
	}
	elsif ( $zeile =~ /^gegen$/i ) { $start2 = 1; $diff = 1; }
	elsif ( $zeile =~ /^boegen$/i ) { setboegen(1); }
	elsif ( $zeile =~ /^hyperbel$/i ) { $hyperbel = 1; }

	# Alle anderen Befehle sind Schrott
	else { printf( "%% Unbekannter Befehl '%s'\n", $zeile ); }
}
}
seterreger(
getabstand(), getwelleeins(), getwellezwei(), getkreisanzahl(),
getliniendicke()
);
erzeugekreise( -$e, getwelleeins(), $start1, getkreisanzahl() );
erzeugekreise( $e, getwellezwei(), $start2, getkreisanzahl() );
if ( $hyperbel == 1 ) {
hyperbel( $e, getwelleeins(), getwellezwei(), 1000 );
}
$leer = 1;
my $layer;
for ( $layer = 0 ; $layer <= 100 ; $layer++ ) {

for ( $i = 0 ; $i < $ausgabedateizeilen[$layer] ; $i++ ) {
	$leer = 0;
}
}
if ( $leer == 0 ) {
kopfdatei();
fussdatei();
for ( $layer = 0 ; $layer <= 11 ; $layer++ ) {
	for ( $i = 0 ; $i < $ausgabedateizeilen[$layer] ; $i++ ) {
		printf( "%s \n", $ausgabedatei[$layer][$i] );
	}
}
}
else { printf("%% Die Datei ist leer \n"); }


1: Siehe [Verschiedene, 2010a] und [Verschiedene, 2010b]

Literatur

[Bronštejn . Semendjaev, 1985]: Bronštejn, Il’ja . K. A. Semendjaev (1985). Taschenbuch der Mathematik. Teubner [u.a.], Leipzig [u.a.], 22 .
[Grehn . Krause, 1998]: Grehn, Joachim . J. Krause (1998). Metzler Physik Sekundarstufe II - 3. Auflage: Metzler Physik (3. A.). Gesamtband.. Schroedel, 3. A., 3. Nachdruck 2000. .
[Tipler, 2000]: Tipler, Paul (2000). Physik. Spektrum Akad. Verl., Heidelberg [u.a.], 3., korrigierter Nachdr. der 1. Aufl. 1994. .
[Verschiedene, 2010a]: Verschiedene (2010a). Ellipse. http://de.wikipedia.org/wiki/Ellipse.
[Verschiedene, 2010b]: Verschiedene (2010b). Hyperbel (Mathematik). http://de.wikipedia.org/wiki/Hyperbel_(Mathematik).

Letzte Änderung: 18.03.2010: 19:19:12 von X. Rendtel