Skript zum Thema Rechnen wie Adam Ries

Diese Seite als pdf-Datei und die kompletten Dateien.

Inhaltsverzeichnis

Skript zum Thema Rechnen wie Adam Ries

1.1 Motivation

Im Schuljahr 2009/2010 habe ich wieder eine fünfte Klasse in Mathematik bekommen. Bisher hatte ich immer bei den Grundrechenarten selbst eine Tabelle in L^AT_EXgesetzt. Aber das musste doch auch automatisch gehen. Wie kann man dies in ein kleines Skript setzen, dass mir alles selbstständig ausgibt? Hierzu habe ich mich mit der Theorie auseinander gesetzt, die ja nun nicht so schwer ist. Schließlich handelt es sich um die Grundrechenarten... Herausgekommen ist mal wieder ein kleines Perl-Skript, mitdem ich L^AT_EX-Code erzeuge für meine gegebene Rechnung.

1.2 Die Theorie

1.2.1 Die schriftliche Addition

Die zu addierenden Zahlen werden so untereinander geschrieben, dass entsprechende Stellen untereinander stehen. Man ordnet die Zahlen rechtsbündig. Nun addiert man nur die letzten Ziffern der Summanden und notiert sich als Zwischenergebnis die letzte Ziffer des Endergebnisses. Ist das Zwischenergebnis mehrstellig, so notiert man sich als Übertrag die weiteren Stellen. Weiter geht es mit zweiten Stelle. Ist ein Übertrag vorhanden, so wird dieser zu den Ziffern der zweiten Stelle hinzuaddiert. Das Zwischenergebnis ist die erste Stelle des Endergebnisses und die zweite Stelle wird erneut als Übertrag notiert. Man fährt so lange bis links fort, bis die Summanden keine weiteren Stellen besitzen.

Beispiel für die schriftliche Addition

Eine Beispielrechnung ist die folgende:

	1	9	0
	5	4	3
	9	8	7
1	2	1


1	7	2	0

Die Rechnungen sind der Reihe nach:

I)	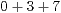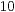Ergebnis 0	Übertrag 1
II)	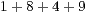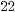Ergebnis 2	Übertrag 2
III)	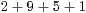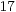Ergebnis 7	Übertrag 1
IV)	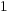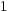Ergebnis 1

1.2.2 Die schriftliche Subtraktion

Die zu subtrahierenden Zahlen werden so unter den Minuenden geschrieben, dass entsprechende Stellen untereinander stehen. Man ordnet die Zahlen rechtsbündig. Nun addiert man nur die letzten Ziffern der Subtrahenden und merkt sich das Zwischenergebnis die letzte Ziffer des Endergebnisses. Ist das Zwischenergebnis mehrstellig, so notiert man sich als Übertrag die weiteren Stellen. Die Differenz von dem Zwischenergebnis zur ersten Ziffer des Minuenden ist das Endergebnis. Analog verfährt man mit den weiteren Stellen, bis es keine stellen mehr gibt.

Beispiel für die schriftliche Subtraktion

Eine Beispielrechnung ist die folgende:

4	3	0	9
2	9	5	6
	4	7	3
2	2


	8	8	0

Die Rechnungen sind der Reihe nach:

I)	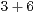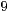Ergänze 0
II)	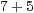Ergänze 8	Übertrag 2
III)	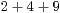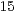Ergänze 8	Übertrag 2
IV)	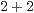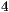Ergänze 0

1.2.3 Die schriftliche Multiplikation

Die zu multiplizierenden Zahlen werden nebeneinander geschrieben. Der zweite Faktor wird in seine einzelnen Ziffern zerlegt. Man multipliziert den ersten Faktor mit der ersten Ziffer und schreibt dieses Ergebnis unter die erste Ziffer des zweiten Faktors rechtsbündig. Analog verfährt man, bis man alle Ziffern des zweiten Faktors abgearbeitet hat. Zu guter letzt werden alle Ergebnisse miteinander addiert.

Beispiel für die schriftliche Multiplikation

Eine Beispielrechnung ist die folgende:

1	2	3		1	9	3

		1	2	3			Multiplikation mit 1
		1	1	0	7		Multiplikation mit 9
				3	6	9	Multiplikation mit 3
				1



		2	3	7	3	9	Addition

1.2.4 Die schriftliche Division

Im Folgenden wird nur die Division mit Rest behandelt. Ich führe hier einmal ein Beispiel für den Algorithmus an:

8	2	9	3	2	7	6	R	1
6									8 geteilt durch 3 ist 6 Rest 2

2	2
2	1								22 geteilt durch 3 ist 21 Rest 1

	1	9
	1	8							19 geteilt durch 3 ist 18 Rest 1

		1

1.3 Der Programmcode

Hier führe ich einmal nur die einzelnen Algorithmen auf für die Grundrechenarten. Das komplette Programm kann auf meiner Homepage http://www.rendtel.de runtergeladen werden.

1.3.1 Die Addition

addition-pm.pm
my $summe; sub setsumme { my ($ergebnis) = @_; $summe = $ergebnis; } sub setaddition { my ($summand) = @_; $summe = $summe + $summand; } sub getsumme { return $summe; } ## Die Summanden werden eingelesen sub addiereneinlesen { my ( $nummer, $summand, $summandexp ) = @_; my $stellensummand; if ( $summandexp >= 0 ) { $stellensummand = vorkommastellen( $summand * 10*$summandexp ); } else { $stellensummand = vorkommastellen($summand); if ( $stellensummand <= abs($summandexp) ) { $stellensummand = abs($summandexp) + 1; } } setspaltenanzahl( $stellensummand + 1 ); schreibezahlintabelle( $summand, $summandexp, $nummer, $stellensummand ); setaddition( $summand 10**$summandexp ); setspaltenanzahl( vorkommastellen( getsumme() ) ); } ## Die Rechnungen fuer die Addtiom finden statt sub addierenauslesen { my ($anzahlzeilen) = @_; my ( $j, $i, $speicherzahl ); for ( $i = 1 ; $i <= $anzahlzeilen ; $i++ ) { for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) { $speicherzahl = zusammensetzen( $i, 1, $j ); } for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) { schreibezelle( "", $i, $j ); } schreibezahlintabelle( $speicherzahl, 0, $i, getspaltenanzahl() ); if ( $i > 1 ) { schreibezelle( "\$+\$", $i, 1 ); } } my $uebertrag = 0; my $teilsumme = 0; for ( $i = getspaltenanzahl() ; $i > 0 ; $i-- ) { for ( $j = 1 ; $j <= $anzahlzeilen ; $j++ ) { if ( ( $rechne[$j][$i] eq "" ) \|\| ( $rechne[$j][$i] eq "\$+\$" ) ) { $teilsumme = $teilsumme; } else { $teilsumme += $rechne[$j][$i]; } $uebertrag = ( $teilsumme - ( $teilsumme % 10 ) ) / 10; if ( $uebertrag == 0 ) { $rechne[ $anzahlzeilen + 1 ][ $i - 1 ] = ""; } else { $rechne[ $anzahlzeilen + 1 ][ $i - 1 ] = "\\tiny{" . $uebertrag . "}"; } $rechne[ $anzahlzeilen + 2 ][$i] = $teilsumme % 10; } $teilsumme = $uebertrag; } for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) { schreibezelle( "", $anzahlzeilen + 2, $j ); } schreibezahlintabelle( getsumme(), 0, $anzahlzeilen + 2, getspaltenanzahl() ); for ( $i = 1 ; $i <= $anzahlzeilen + 1 ; $i++ ) { lesetabellenzeile( $i, getspaltenanzahl() ); } ausgabe("\\hline \\hline"); lesetabellenzeile( $anzahlzeilen + 2, getspaltenanzahl() ); }

addition-pm.pm

my $summe;
sub setsumme {
	my ($ergebnis) = @_;
	$summe = $ergebnis;
}
sub setaddition {
	my ($summand) = @_;
	$summe = $summe + $summand;
}
sub getsumme { return $summe; }
## Die Summanden werden eingelesen
sub addiereneinlesen {
	my ( $nummer, $summand, $summandexp ) = @_;
	my $stellensummand;
	if ( $summandexp >= 0 ) {
		$stellensummand = vorkommastellen( $summand * 10**$summandexp );
	}
	else {
		$stellensummand = vorkommastellen($summand);
		if ( $stellensummand <= abs($summandexp) ) {
			$stellensummand = abs($summandexp) + 1;
		}
	}
	setspaltenanzahl( $stellensummand + 1 );
	schreibezahlintabelle( $summand, $summandexp, $nummer, $stellensummand );
	setaddition( $summand * 10**$summandexp );
	setspaltenanzahl( vorkommastellen( getsumme() ) );
}
## Die Rechnungen fuer die Addtiom finden statt
sub addierenauslesen {
	my ($anzahlzeilen) = @_;
	my ( $j, $i, $speicherzahl );
	for ( $i = 1 ; $i <= $anzahlzeilen ; $i++ ) {
		for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) {
			$speicherzahl = zusammensetzen( $i, 1, $j );
		}
		for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) {
			schreibezelle( "", $i, $j );
		}
		schreibezahlintabelle( $speicherzahl, 0, $i, getspaltenanzahl() );
		if ( $i > 1 ) { schreibezelle( "\$+\$", $i, 1 ); }
	}
	my $uebertrag = 0;
	my $teilsumme = 0;
	for ( $i = getspaltenanzahl() ; $i > 0 ; $i-- ) {
		for ( $j = 1 ; $j <= $anzahlzeilen ; $j++ ) {
			if ( ( $rechne[$j][$i] eq "" )
				|| ( $rechne[$j][$i] eq "\$+\$" ) )
			{
				$teilsumme = $teilsumme;
			}
			else { $teilsumme += $rechne[$j][$i]; }
			$uebertrag = ( $teilsumme - ( $teilsumme % 10 ) ) / 10;
			if ( $uebertrag == 0 ) {
				$rechne[ $anzahlzeilen + 1 ][ $i - 1 ] = "";
			}
			else {
				$rechne[ $anzahlzeilen + 1 ][ $i - 1 ] = "\\tiny{" . $uebertrag . "}";
			}
			$rechne[ $anzahlzeilen + 2 ][$i] = $teilsumme % 10;
		}
		$teilsumme = $uebertrag;
	}
	for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) {
		schreibezelle( "", $anzahlzeilen + 2, $j );
	}
	schreibezahlintabelle( getsumme(), 0, $anzahlzeilen + 2, getspaltenanzahl() );
	for ( $i = 1 ; $i <= $anzahlzeilen + 1 ; $i++ ) {
		lesetabellenzeile( $i, getspaltenanzahl() );
	}
	
	ausgabe("\\hline \\hline");
	lesetabellenzeile( $anzahlzeilen + 2, getspaltenanzahl() );
}

1.3.2 Die Subtraktion

subtraktion-pm.pm
my $differenz = 0; sub setdifferenz { my ($ergebnis) = @_; $differenz = $ergebnis; } sub setsubtraktion { my ($subtrahend) = @_; $differenz = $differenz - $subtrahend; } sub getdifferenz { return $differenz;} sub subtrahiereneinlesen { my ( $nummer, $summand, $summandexp ) = @_; my ($stellensummand); if ( $summandexp >= 0 ) { $stellensummand = vorkommastellen( $summand * 10*$summandexp ); } else { $stellensummand = vorkommastellen($summand); if ( $stellensummand <= abs($summandexp) ) { $stellensummand = abs($summandexp) + 1; } } setspaltenanzahl( $stellensummand + 1 ); schreibezahlintabelle( $summand, $summandexp, $nummer, $stellensummand ); if ( $nummer > 1 ) { setsubtraktion( $summand 10*$summandexp ); setaddition( $summand 10*$summandexp ); } else { schreibezahlintabelle( $summand, $summandexp, 0, $stellensummand ); setsumme(0); setdifferenz( $summand 10**$summandexp ); } setspaltenanzahl( vorkommastellen( getdifferenz() ) ); } sub subtrahierenauslesen { my ($anzahlzeilen) = @_; my ( $j, $i, $speicherzahl, $uebertrag, $teilsumme, $teildifferenz, $minuend ); for ( $i = 0 ; $i <= $anzahlzeilen ; $i++ ) { for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) { $speicherzahl = zusammensetzen( $i, 1, $j ); } for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) { schreibezelle( "", $i, $j ); } schreibezahlintabelle( $speicherzahl, 0, $i, getspaltenanzahl() ); if ( $i > 1 ) { schreibezelle( "\$-\$", $i, 1 );} } for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) { schreibezelle( "", $anzahlzeilen + 2, $j ); } for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) { schreibezahlintabelle( 0, 0, $anzahlzeilen + 1, $j ); schreibezahlintabelle( 0, 0, $anzahlzeilen + 3, $j ); schreibezahlintabelle( 0, 0, $anzahlzeilen + 5, $j ); } schreibezahlintabelle( getsumme(), 0, $anzahlzeilen + 3, getspaltenanzahl() ); schreibezahlintabelle( getdifferenz(), 0, $anzahlzeilen + 4, getspaltenanzahl() ); for ( $i = 1 ; $i <= $anzahlzeilen ; $i++ ) { lesetabellenzeile( $i, getspaltenanzahl() ); } $uebertrag = $teilsumme = 0; for ( $i = getspaltenanzahl() ; $i > 0 ; $i-- ) { for ( $j = 2 ; $j <= $anzahlzeilen ; $j++ ) { if ( ( $rechne[$j][$i] eq "" ) \|\| ( $rechne[$j][$i] eq "\$-\$" ) ) {$teilsumme = $teilsumme; } else {$teilsumme += $rechne[$j][$i];} $uebertrag = ( $teilsumme - ( $teilsumme % 10 ) ) / 10; if ( $uebertrag == 0 ) { $rechne[ $anzahlzeilen + 1 ][ $i - 1 ] = 0; } else {$rechne[ $anzahlzeilen + 1 ][ $i - 1 ] = $uebertrag;} $rechne[ $anzahlzeilen + 2 ][$i] = $teilsumme % 10; } $teilsumme = $uebertrag; } $teildifferenz = $minuend = 0; for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) { $minuend = zusammensetzen( 0, 1, $j ); } for ( $j = getspaltenanzahl() ; $j > getspaltenanzahl() - vorkommastellen($minuend) ; $j-- ) { $teildifferenz = $rechne[0][$j] - $rechne[ $anzahlzeilen + 3 ][$j]; if ( $teildifferenz >= 0 ) { $rechne[ $anzahlzeilen + 5 ][ $j - 1 ] = $rechne[ $anzahlzeilen + 1 ][ $j - 1 ] + 0; } else { $rechne[ $anzahlzeilen + 5 ][ $j - 1 ] = $rechne[ $anzahlzeilen + 1 ][ $j - 1 ] + 1; } } for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) { if ( $rechne[ $anzahlzeilen + 5 ][$j] == 0 ) { $rechne[ $anzahlzeilen + 5 ][$j] = ""; } else { $rechne[ $anzahlzeilen + 5 ][$j] = "\\tiny{" . $rechne[ $anzahlzeilen + 5 ][$j] . "}"; } } lesetabellenzeile( $anzahlzeilen + 5, getspaltenanzahl() ); ausgabe("\\hline \\hline"); lesetabellenzeile( $anzahlzeilen + 4, getspaltenanzahl() ); }

subtraktion-pm.pm

my $differenz = 0;
sub setdifferenz {
my ($ergebnis) = @_;
$differenz = $ergebnis;
}
sub setsubtraktion {
my ($subtrahend) = @_;
$differenz = $differenz - $subtrahend;
}
sub getdifferenz { return $differenz;}
sub subtrahiereneinlesen {
my ( $nummer, $summand, $summandexp ) = @_;
my ($stellensummand);
if ( $summandexp >= 0 ) {
	$stellensummand = vorkommastellen( $summand * 10**$summandexp );
}
else {
	$stellensummand = vorkommastellen($summand);
	if ( $stellensummand <= abs($summandexp) ) {
	 $stellensummand = abs($summandexp) + 1;
	}
}
setspaltenanzahl( $stellensummand + 1 );
schreibezahlintabelle( $summand, $summandexp, $nummer, $stellensummand );
if ( $nummer > 1 ) {
	setsubtraktion( $summand * 10**$summandexp );
	setaddition( $summand * 10**$summandexp );
}
else {
	schreibezahlintabelle( $summand, $summandexp, 0, $stellensummand );
	setsumme(0);
	setdifferenz( $summand * 10**$summandexp );
}
setspaltenanzahl( vorkommastellen( getdifferenz() ) );
}
sub subtrahierenauslesen {
my ($anzahlzeilen) = @_;
my ( $j, $i, $speicherzahl, $uebertrag, $teilsumme, $teildifferenz, $minuend );
for ( $i = 0 ; $i <= $anzahlzeilen ; $i++ ) {
	for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) {
	 $speicherzahl = zusammensetzen( $i, 1, $j );
	}
	for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) {
	 schreibezelle( "", $i, $j );
	}
	schreibezahlintabelle( $speicherzahl, 0, $i, getspaltenanzahl() );
	if ( $i > 1 ) {	 schreibezelle( "\$-\$", $i, 1 );}
}
for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) {
	schreibezelle( "", $anzahlzeilen + 2, $j );
}
for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) {
	schreibezahlintabelle( 0, 0, $anzahlzeilen + 1, $j );
	schreibezahlintabelle( 0, 0, $anzahlzeilen + 3, $j );
	schreibezahlintabelle( 0, 0, $anzahlzeilen + 5, $j );
}
schreibezahlintabelle( getsumme(), 0, $anzahlzeilen + 3, getspaltenanzahl() );
schreibezahlintabelle( getdifferenz(), 0, $anzahlzeilen + 4, getspaltenanzahl() );
for ( $i = 1 ; $i <= $anzahlzeilen ; $i++ ) {
	lesetabellenzeile( $i, getspaltenanzahl() );
}
$uebertrag = $teilsumme = 0;
for ( $i = getspaltenanzahl() ; $i > 0 ; $i-- ) {
	for ( $j = 2 ; $j <= $anzahlzeilen ; $j++ ) {
	 if ( ( $rechne[$j][$i] eq "" )
		 || ( $rechne[$j][$i] eq "\$-\$" ) )
	 {$teilsumme = $teilsumme; }
	 else {$teilsumme += $rechne[$j][$i];}
	 $uebertrag = ( $teilsumme - ( $teilsumme % 10 ) ) / 10;
	 if ( $uebertrag == 0 ) {
		$rechne[ $anzahlzeilen + 1 ][ $i - 1 ] = 0;
	 }
	 else {$rechne[ $anzahlzeilen + 1 ][ $i - 1 ] = $uebertrag;}
	 $rechne[ $anzahlzeilen + 2 ][$i] = $teilsumme % 10;
	}
	$teilsumme = $uebertrag;
}
$teildifferenz = $minuend = 0;
for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) {
	$minuend = zusammensetzen( 0, 1, $j );
}
for ( $j = getspaltenanzahl() ; $j > getspaltenanzahl() - vorkommastellen($minuend) ; $j-- ) {
	$teildifferenz = $rechne[0][$j] - $rechne[ $anzahlzeilen + 3 ][$j];
	if ( $teildifferenz >= 0 ) {
	 $rechne[ $anzahlzeilen + 5 ][ $j - 1 ] = $rechne[ $anzahlzeilen + 1 ][ $j - 1 ] + 0;
	}
	else {
	 $rechne[ $anzahlzeilen + 5 ][ $j - 1 ] = $rechne[ $anzahlzeilen + 1 ][ $j - 1 ] + 1;
	}
}
for ( $j = 1 ; $j <= getspaltenanzahl() ; $j++ ) {
	if ( $rechne[ $anzahlzeilen + 5 ][$j] == 0 ) {
	 $rechne[ $anzahlzeilen + 5 ][$j] = "";
	}
	else {
	 $rechne[ $anzahlzeilen + 5 ][$j] = "\\tiny{" . $rechne[ $anzahlzeilen + 5 ][$j] . "}";
	}
}
lesetabellenzeile( $anzahlzeilen + 5, getspaltenanzahl() );
ausgabe("\\hline \\hline");
lesetabellenzeile( $anzahlzeilen + 4, getspaltenanzahl() );
}

1.3.3 Die Multiplikation

multiplikation-pm.pm
sub multipliziere { my ( $faktoreins, $faktoreinsexp, $faktorzwei, $faktorzweiexp ) = @_; my ( $stellenfaktoreins, $stellenfaktorzwei, $stellengesamt, $ergebnis, $zeilen, $vorzeichenfaktoreins, $vorzeichenfaktorzwei, $stellenergebnis, $faktorzweispeicher ); ## Haben die Zahlen ein negatives Vorzeichen? if ( $faktorzwei < 0 ) {$vorzeichenfaktorzwei = 1; } else { $vorzeichenfaktorzwei = 0; } if ( $faktoreins < 0 ) { $vorzeichenfaktoreins = 1; } else { $vorzeichenfaktoreins = 0; } $faktoreins = abs($faktoreins); $faktorzweispeicher = $faktorzwei = abs($faktorzwei); ## Vor- oder Nachkommastellen? if ( $faktoreinsexp >= 0 ) { $stellenfaktoreins = vorkommastellen( $faktoreins * 10*$faktoreinsexp ); } else { $stellenfaktoreins = vorkommastellen($faktoreins); if ( $stellenfaktoreins <= abs($faktoreinsexp) ) { $stellenfaktoreins = abs($faktoreinsexp) + 1; } } if ( $faktorzweiexp >= 0 ) { $stellenfaktorzwei = vorkommastellen( $faktorzwei 10*$faktorzweiexp ); } else { $stellenfaktorzwei = vorkommastellen($faktorzwei); if ( $stellenfaktorzwei <= abs($faktorzweiexp) ) { $stellenfaktorzwei = abs($faktorzweiexp) + 1; } } if ( $faktoreinsexp + $faktorzweiexp >= 0 ) { $stellenergebnis = vorkommastellen( $faktorzwei 10*$faktorzweiexp $faktoreins * 10*$faktoreinsexp ); } else { $stellenergebnis = vorkommastellen( $faktorzwei $faktoreins ); } $stellengesamt = $stellenfaktoreins + 1 + $stellenfaktorzwei + $vorzeichenfaktoreins + $vorzeichenfaktorzwei; ## Die erste Zeile wird geschrieben ## Was ist zu rechnen tabellenkopf($stellengesamt); if ( $vorzeichenfaktoreins == 1 ) { schreibezelle( "\$-\$", 1, 1 ); } schreibezahlintabelle( $faktoreins, $faktoreinsexp, 1, $stellenfaktoreins + $vorzeichenfaktoreins ); schreibezelle( "\$\\cdot\$", 1, $stellenfaktoreins + 1 + $vorzeichenfaktoreins ); if ( $vorzeichenfaktorzwei == 1 ) { schreibezelle( "\$-\$", 1, $stellenfaktoreins + 1 + $vorzeichenfaktoreins + $vorzeichenfaktorzwei ); } schreibezahlintabelle( $faktorzwei, $faktorzweiexp, 1, $stellenfaktoreins + $vorzeichenfaktoreins + 1 + $stellenfaktorzwei + $vorzeichenfaktorzwei ); lesetabellenzeile( 1, $stellengesamt ); ausgabe("\\hline"); $zeilen = 1; my $wieoftmultipliziere = vorkommastellen($faktorzwei); my $i = 1; my $j = 0; for ( $i = 1 + $stellenfaktorzwei ; $i > 1 ; $i-- ) { if ( $faktoreinsexp >= 0 ) { $ergebnis = $faktoreins * 10*$faktoreinsexp ( $faktorzwei % 10 ); } else { $ergebnis = $faktoreins * ( $faktorzwei % 10 ); } schreibezahlintabelle( $ergebnis, 0, $i, $stellengesamt - $j ); $faktorzwei = ( $faktorzwei - ( $faktorzwei % 10 ) ) / 10; $j++; $zeilen++; } $faktorzwei = $faktorzweispeicher; for ( $i = 2 ; $i <= $stellenfaktorzwei + 1 ; $i++ ) { lesetabellenzeile( $i, $stellengesamt ); } schreibezahlintabelle( $faktoreins * $faktorzwei, $faktoreinsexp + $faktorzweiexp, $zeilen + 3, $stellengesamt ); ## Der Uebertrag wird bestimmt my $uebertrag = 0; my $teilsumme = 0; for ( $i = $stellengesamt ; $i > 0 ; $i-- ) { for ( $j = 2 ; $j <= $zeilen ; $j++ ) { if ( $rechne[$j][$i] eq "" ) { $teilsumme = $teilsumme; } else { $teilsumme += $rechne[$j][$i]; } $uebertrag = ( $teilsumme - ( $teilsumme % 10 ) ) / 10; if ( $uebertrag == 0 ) { $rechne[ $zeilen + 1 ][ $i - 1 ] = ""; } else { $rechne[ $zeilen + 1 ][ $i - 1 ] = "\\tiny{" . $uebertrag . "}"; } $rechne[ $zeilen + 2 ][$i] = $teilsumme % 10; } $teilsumme = $uebertrag; } ## Das Rechenergebnis wird bestimmt lesetabellenzeile( $zeilen + 1, $stellengesamt ); schreibezahlintabelle( $faktoreins * $faktorzwei, $faktoreinsexp + $faktorzweiexp, $zeilen + 3, $stellengesamt ); ausgabe("\\hline \\hline"); if ( ( $vorzeichenfaktoreins + $vorzeichenfaktorzwei ) == 1 ) { schreibezelle( "\$-\$", $zeilen + 3, $stellengesamt - ($stellenergebnis) ); } lesetabellenzeile( $zeilen + 3, $stellengesamt ); tabellenfuss(); }

multiplikation-pm.pm

sub multipliziere {
my ( $faktoreins, $faktoreinsexp, $faktorzwei, $faktorzweiexp ) = @_;
my ( $stellenfaktoreins, $stellenfaktorzwei, $stellengesamt, $ergebnis,
	 $zeilen, $vorzeichenfaktoreins, $vorzeichenfaktorzwei,
	 $stellenergebnis, $faktorzweispeicher );
## Haben die Zahlen ein negatives Vorzeichen?
if ( $faktorzwei < 0 ) {$vorzeichenfaktorzwei = 1; }
else {	$vorzeichenfaktorzwei = 0; }
if ( $faktoreins < 0 ) {	$vorzeichenfaktoreins = 1; }
else {	$vorzeichenfaktoreins = 0; }
$faktoreins = abs($faktoreins);
$faktorzweispeicher = $faktorzwei = abs($faktorzwei);
## Vor- oder Nachkommastellen?
if ( $faktoreinsexp >= 0 ) {
	$stellenfaktoreins = vorkommastellen( $faktoreins * 10**$faktoreinsexp );
}
else {
	$stellenfaktoreins = vorkommastellen($faktoreins);
	if ( $stellenfaktoreins <= abs($faktoreinsexp) ) {
	 $stellenfaktoreins = abs($faktoreinsexp) + 1;
	}
}
if ( $faktorzweiexp >= 0 ) {
	$stellenfaktorzwei = vorkommastellen( $faktorzwei * 10**$faktorzweiexp );
}
else {
	$stellenfaktorzwei = vorkommastellen($faktorzwei);
	if ( $stellenfaktorzwei <= abs($faktorzweiexp) ) {
	 $stellenfaktorzwei = abs($faktorzweiexp) + 1;
	}
}
if ( $faktoreinsexp + $faktorzweiexp >= 0 ) {
	$stellenergebnis =
	 vorkommastellen( $faktorzwei * 10**$faktorzweiexp * $faktoreins * 10**$faktoreinsexp );
}
else { $stellenergebnis = vorkommastellen( $faktorzwei * $faktoreins ); }
$stellengesamt =
	$stellenfaktoreins + 1 + $stellenfaktorzwei + $vorzeichenfaktoreins + $vorzeichenfaktorzwei;
## Die erste Zeile wird geschrieben
## Was ist zu rechnen
tabellenkopf($stellengesamt);
if ( $vorzeichenfaktoreins == 1 ) { schreibezelle( "\$-\$", 1, 1 ); }
schreibezahlintabelle( $faktoreins, $faktoreinsexp, 1,
			 $stellenfaktoreins + $vorzeichenfaktoreins );
schreibezelle( "\$\\cdot\$", 1, $stellenfaktoreins + 1 + $vorzeichenfaktoreins );
if ( $vorzeichenfaktorzwei == 1 ) {
	schreibezelle( "\$-\$", 1,
		 $stellenfaktoreins + 1 + $vorzeichenfaktoreins + $vorzeichenfaktorzwei );
}
schreibezahlintabelle( $faktorzwei, $faktorzweiexp, 1,
			 $stellenfaktoreins + $vorzeichenfaktoreins + 1 + $stellenfaktorzwei +
			 $vorzeichenfaktorzwei );
lesetabellenzeile( 1, $stellengesamt );
ausgabe("\\hline");
$zeilen = 1;
my $wieoftmultipliziere = vorkommastellen($faktorzwei);
my $i = 1;
my $j = 0;
for ( $i = 1 + $stellenfaktorzwei ; $i > 1 ; $i-- ) {
	if ( $faktoreinsexp >= 0 ) {
	 $ergebnis = $faktoreins * 10**$faktoreinsexp * ( $faktorzwei % 10 );
	}
	else {
	 $ergebnis = $faktoreins * ( $faktorzwei % 10 );
	}
	schreibezahlintabelle( $ergebnis, 0, $i, $stellengesamt - $j );
	$faktorzwei = ( $faktorzwei - ( $faktorzwei % 10 ) ) / 10;
	$j++;
	$zeilen++;
}
$faktorzwei = $faktorzweispeicher;
for ( $i = 2 ; $i <= $stellenfaktorzwei + 1 ; $i++ ) {
	lesetabellenzeile( $i, $stellengesamt );
}
schreibezahlintabelle( $faktoreins * $faktorzwei, $faktoreinsexp +
			 $faktorzweiexp, $zeilen + 3, $stellengesamt );
## Der Uebertrag wird bestimmt
my $uebertrag = 0;
my $teilsumme = 0;
for ( $i = $stellengesamt ; $i > 0 ; $i-- ) {
	for ( $j = 2 ; $j <= $zeilen ; $j++ ) {
	 if ( $rechne[$j][$i] eq "" ) {
		$teilsumme = $teilsumme;
	 }
	 else {
		$teilsumme += $rechne[$j][$i];
	 }
	 $uebertrag = ( $teilsumme - ( $teilsumme % 10 ) ) / 10;
	 if ( $uebertrag == 0 ) {
		$rechne[ $zeilen + 1 ][ $i - 1 ] = "";
	 }
	 else {
		$rechne[ $zeilen + 1 ][ $i - 1 ] = "\\tiny{" . $uebertrag . "}";
	 }
	 $rechne[ $zeilen + 2 ][$i] = $teilsumme % 10;
	}
	$teilsumme = $uebertrag;
}
## Das Rechenergebnis wird bestimmt
lesetabellenzeile( $zeilen + 1, $stellengesamt );
schreibezahlintabelle(
	$faktoreins * $faktorzwei,
	$faktoreinsexp + $faktorzweiexp,
	$zeilen + 3,
	$stellengesamt
	);
ausgabe("\\hline \\hline");
if ( ( $vorzeichenfaktoreins + $vorzeichenfaktorzwei ) == 1 ) {
	schreibezelle( "\$-\$", $zeilen + 3, $stellengesamt - ($stellenergebnis) );
}
lesetabellenzeile( $zeilen + 3, $stellengesamt );
tabellenfuss();
}

1.3.4 Die Division

division-pm.pm
sub dividiere { my ( $dividend, $dividendexp, $divisor, $divisorexp ) = @_; my ( $stellendividend, $stellendivisor, $stellengesamt, $ergebnis, $zeilen, $vorzeichendividend, $vorzeichendivisor, $stellenergebnis, $ende, $zwischenergebnis, $i, $merkezahl, $differenz, $starte, $rest, $reststellen ); if ( $divisorexp < 0 ) { $rest = ( ( $dividend * 10*$dividendexp 10*( -$divisorexp ) ) % ( $divisor 10*$divisorexp 10*( -$divisorexp ) ) ); } else { $rest = ( ( $dividend 10*$dividendexp ) % ( $divisor 10*$divisorexp ) ); } if ( $rest != 0 ) { $reststellen = vorkommastellen($rest) + 1; } else { $reststellen = 0; } my @ergebnisvektor = (); for ( $i = 0 ; $i <= 100 ; $i++ ) { $ergebnisvektor[$i] = ""; } ## Haben die Zahlen ein negatives Vorzeichen? if ( $divisor < 0 ) { $vorzeichendivisor = 1; } else { $vorzeichendivisor = 0; } if ( $dividend < 0 ) { $vorzeichendividend = 1; } else { $vorzeichendividend = 0; } $dividend = abs($dividend); $divisor = abs($divisor); ## Vor- oder Nachkommastellen? if ( $dividendexp >= 0 ) { $stellendividend = vorkommastellen( $dividend 10*$dividendexp ); } else { $stellendividend = vorkommastellen($dividend); if ( $stellendividend <= abs($dividendexp) ) { $stellendividend = abs($dividendexp) + 1; } } if ( $divisorexp >= 0 ) { $stellendivisor = vorkommastellen( $divisor 10*$divisorexp ); } else { $stellendivisor = vorkommastellen($divisor); if ( $stellendivisor <= abs($divisorexp) ) { $stellendivisor = abs($divisorexp) + 1; } } if ( $dividendexp - $divisorexp >= 0 ) { $stellenergebnis = vorkommastellen( ( $dividend 10*$dividendexp ) / ( $divisor 10*$divisorexp ) ); } else { $stellenergebnis = vorkommastellen( $dividend / $divisor ); if ( $stellenergebnis <= abs( $dividendexp - $divisorexp ) ) { $stellenergebnis = abs( $dividendexp - $divisorexp ) + 1; } } $stellengesamt = $stellendividend + 1 + $stellendivisor + $vorzeichendividend + $vorzeichendivisor + 1 + $stellenergebnis + $reststellen; ## Der Tabellenkopf wird geschrieben, wie viele Stellen sind vorhanden. tabellenkopf($stellengesamt); ## Die erste Zeile wird geschrieben ## Was ist zu rechnen if ( $vorzeichendividend == 1 ) { schreibezelle( "\$-\$", 1, 1 ); } schreibezahlintabelle( $dividend, $dividendexp, 1, $stellendividend + $vorzeichendividend ); ## fuer Zwischenrechnungen for ( $i = 0 ; $i < 100 ; $i++ ) { schreibezahlintabelle( 0, 0, 0, $i ); } schreibezahlintabelle( $dividend, $dividendexp, 0, $stellendividend + $vorzeichendividend ); schreibezelle( "\$:\$", 1, $stellendividend + 1 + $vorzeichendividend ); if ( $vorzeichendivisor == 1 ) { schreibezelle( "\$-\$", 1, $stellendividend + 1 + $vorzeichendividend + $vorzeichendivisor ); } schreibezahlintabelle( $divisor, $divisorexp, 1, $stellendividend + $vorzeichendividend + 1 + $stellendivisor + $vorzeichendivisor ); schreibezelle( "\$=\$", 1, $stellendividend + 1 + $vorzeichendividend + $vorzeichendivisor + $stellendivisor + 1 ); schreibezahlintabelle( $dividend / $divisor, $dividendexp - $divisorexp, 1, $stellengesamt - $reststellen ); if ( $rest != 0 ) { schreibezelle( "R", 1, $stellengesamt - ( $reststellen - 1 ) ); schreibezahlintabelle( $rest, 0, 1, $stellengesamt ); } $zeilen = 1; lesetabellenzeile( 1, $stellengesamt ); if ( $dividendexp > 0 ) { $dividend = $dividend 10*$dividendexp; } if ( $divisorexp > 0 ) { $divisor = $divisor 10*$divisorexp; } if ( $divisorexp < 0 ) { $divisor = $divisor 10*( -$divisorexp ) 10*($divisorexp); $dividend = $dividend 10*( -$divisorexp ); } for ( $i = 0 ; $i < $stellenergebnis ; $i++ ) { $ergebnisvektor[ $stellenergebnis - $i ] = zusammensetzen( 1, $stellengesamt - $reststellen - $i, $stellengesamt - $reststellen - $i ); } $ende = $differenz = $starte = 0; $zeilen++; my $anfang = 1; my $start = 1; for ( $j = 1 ; $j <= $stellengesamt ; $j++ ) { if ( teilersein( zusammensetzen( 0, $anfang, $j ), int( $ergebnisvektor[1] $divisor ) ) == 1 ) { if ( $starte == 0 ) { $merkezahl = zusammensetzen( 0, $anfang, $j ); $starte = 1; $ende = $j; } } } for ( $i = 1 ; $i <= $stellenergebnis ; $i++ ) { $zwischenergebnis = int( $ergebnisvektor[$i] * $divisor ); if ( $ergebnisvektor[$i] != 0 ) { $differenz = $merkezahl - $zwischenergebnis; for ( $j = 1 ; $j <= $ende ; $j++ ) { schreibezahlintabelle( 0, 0, 0, $j ); } schreibezahlintabelle( $differenz, 0, 0, $ende ); if ( $i > 1 ) { schreibezahlintabelle( $merkezahl, 0, $zeilen, $ende ); lesetabellenzeile( $zeilen, $stellengesamt ); $zeilen++; schreibezahlintabelle( $differenz, 0, 0, $ende ); } if ( $zwischenergebnis != 0 ) { schreibezahlintabelle( $zwischenergebnis, 0, $zeilen, $ende ); lesetabellenzeile( $zeilen, $stellengesamt ); ausgabe( "\\cline{" . $start . "-" . $ende . "}" ); $zeilen++; schreibezahlintabelle( $differenz, 0, $zeilen, $ende ); } } $ende++; $merkezahl = zusammensetzen( 0, $anfang, $ende ); $starte = 0; for ( $j = 1 ; $j <= $ende ; $j++ ) { if ( zusammensetzen( 0, $j, $j ) == 0 ) { if ( $starte == 0 ) { $start = $j + 1; } } else { $starte = 1; } } } $zeilen++; $ende = vorkommastellen($dividend); schreibezahlintabelle( $rest, 0, $zeilen, $ende ); lesetabellenzeile( $zeilen, $stellengesamt ); tabellenfuss(); }

division-pm.pm

sub dividiere {
my ( $dividend, $dividendexp, $divisor, $divisorexp ) = @_;
my ( $stellendividend, $stellendivisor, $stellengesamt, $ergebnis,
	 $zeilen, $vorzeichendividend, $vorzeichendivisor, $stellenergebnis,
	 $ende, $zwischenergebnis, $i, $merkezahl, $differenz, $starte, $rest,
	 $reststellen );
if ( $divisorexp < 0 ) {
	$rest =
	 ( ( $dividend * 10**$dividendexp * 10**( -$divisorexp ) ) %
	 ( $divisor * 10**$divisorexp * 10**( -$divisorexp ) ) );
}
else {
	$rest = ( ( $dividend * 10**$dividendexp ) % ( $divisor * 10**$divisorexp ) );
}
if ( $rest != 0 ) {	$reststellen = vorkommastellen($rest) + 1; }
else { $reststellen = 0; }
my @ergebnisvektor = ();
for ( $i = 0 ; $i <= 100 ; $i++ ) {
	$ergebnisvektor[$i] = "";
}
## Haben die Zahlen ein negatives Vorzeichen?
if ( $divisor < 0 ) { $vorzeichendivisor = 1; }
else { $vorzeichendivisor = 0; }
if ( $dividend < 0 ) { $vorzeichendividend = 1; }
else { $vorzeichendividend = 0; }
$dividend = abs($dividend);
$divisor = abs($divisor);
## Vor- oder Nachkommastellen?
if ( $dividendexp >= 0 ) {
	$stellendividend = vorkommastellen( $dividend * 10**$dividendexp );
}
else {
	$stellendividend = vorkommastellen($dividend);
	if ( $stellendividend <= abs($dividendexp) ) {
	 $stellendividend = abs($dividendexp) + 1;
	}
}
if ( $divisorexp >= 0 ) {
	$stellendivisor = vorkommastellen( $divisor * 10**$divisorexp );
}
else {
	$stellendivisor = vorkommastellen($divisor);
	if ( $stellendivisor <= abs($divisorexp) ) {
	 $stellendivisor = abs($divisorexp) + 1;
	}
}
if ( $dividendexp - $divisorexp >= 0 ) {
	$stellenergebnis =
	 vorkommastellen( ( $dividend * 10**$dividendexp ) / ( $divisor * 10**$divisorexp ) );
}
else {
	$stellenergebnis = vorkommastellen( $dividend / $divisor );
	if ( $stellenergebnis <= abs( $dividendexp - $divisorexp ) ) {
	 $stellenergebnis = abs( $dividendexp - $divisorexp ) + 1;
	}
}
$stellengesamt =
	$stellendividend + 1 + $stellendivisor + $vorzeichendividend + $vorzeichendivisor + 1 +
	$stellenergebnis + $reststellen;
## Der Tabellenkopf wird geschrieben, wie viele Stellen sind vorhanden.
tabellenkopf($stellengesamt);
## Die erste Zeile wird geschrieben
## Was ist zu rechnen
if ( $vorzeichendividend == 1 ) {	schreibezelle( "\$-\$", 1, 1 ); }
schreibezahlintabelle( $dividend, $dividendexp, 1, $stellendividend + $vorzeichendividend );
## fuer Zwischenrechnungen
for ( $i = 0 ; $i < 100 ; $i++ ) {
	schreibezahlintabelle( 0, 0, 0, $i );
}
schreibezahlintabelle( $dividend, $dividendexp, 0, $stellendividend + $vorzeichendividend );
schreibezelle( "\$:\$", 1, $stellendividend + 1 + $vorzeichendividend );
if ( $vorzeichendivisor == 1 ) {
	schreibezelle( "\$-\$", 1,
		 $stellendividend + 1 + $vorzeichendividend + $vorzeichendivisor );
}
schreibezahlintabelle( $divisor, $divisorexp, 1,
			 $stellendividend + $vorzeichendividend + 1 + $stellendivisor + $vorzeichendivisor );
schreibezelle( "\$=\$", 1,
		 $stellendividend + 1 + $vorzeichendividend + $vorzeichendivisor + $stellendivisor + 1 );
schreibezahlintabelle(
	$dividend / $divisor,
	$dividendexp - $divisorexp,
	1, $stellengesamt - $reststellen
	);
if ( $rest != 0 ) {
	schreibezelle( "R", 1, $stellengesamt - ( $reststellen - 1 ) );
	schreibezahlintabelle( $rest, 0, 1, $stellengesamt );
}
$zeilen = 1;
lesetabellenzeile( 1, $stellengesamt );
if ( $dividendexp > 0 ) {
	$dividend = $dividend * 10**$dividendexp;
}
if ( $divisorexp > 0 ) {
	$divisor = $divisor * 10**$divisorexp;
}
if ( $divisorexp < 0 ) {
	$divisor = $divisor * 10**( -$divisorexp ) * 10**($divisorexp);
	$dividend = $dividend * 10**( -$divisorexp );
}
for ( $i = 0 ; $i < $stellenergebnis ; $i++ ) {
	$ergebnisvektor[ $stellenergebnis - $i ] = zusammensetzen(
	 1,
	 $stellengesamt - $reststellen - $i,
	 $stellengesamt - $reststellen - $i
	 );
}
$ende = $differenz = $starte = 0;
$zeilen++;
my $anfang = 1;
my $start = 1;
for ( $j = 1 ; $j <= $stellengesamt ; $j++ ) {
	if ( teilersein( zusammensetzen( 0, $anfang, $j ), int( $ergebnisvektor[1] * $divisor ) ) ==
	 1 )
	{
	 if ( $starte == 0 ) {
		$merkezahl = zusammensetzen( 0, $anfang, $j );
		$starte = 1;
		$ende = $j;
	 }
	}
}
for ( $i = 1 ; $i <= $stellenergebnis ; $i++ ) {
	$zwischenergebnis = int( $ergebnisvektor[$i] * $divisor );
	if ( $ergebnisvektor[$i] != 0 ) {
	 $differenz = $merkezahl - $zwischenergebnis;
	 for ( $j = 1 ; $j <= $ende ; $j++ ) {
		schreibezahlintabelle( 0, 0, 0, $j );
	 }
	 schreibezahlintabelle( $differenz, 0, 0, $ende );
	 if ( $i > 1 ) {
		schreibezahlintabelle( $merkezahl, 0, $zeilen, $ende );
		lesetabellenzeile( $zeilen, $stellengesamt );
		$zeilen++;
		schreibezahlintabelle( $differenz, 0, 0, $ende );
	 }
	 if ( $zwischenergebnis != 0 ) {
		schreibezahlintabelle( $zwischenergebnis, 0, $zeilen, $ende );
		lesetabellenzeile( $zeilen, $stellengesamt );
		ausgabe( "\\cline{" . $start . "-" . $ende . "}" );
		$zeilen++;
		schreibezahlintabelle( $differenz, 0, $zeilen, $ende );
	 }
	}
	$ende++;
	$merkezahl = zusammensetzen( 0, $anfang, $ende );
	$starte = 0;
	for ( $j = 1 ; $j <= $ende ; $j++ ) {
	 if ( zusammensetzen( 0, $j, $j ) == 0 ) {
		if ( $starte == 0 ) { $start = $j + 1; }
	 }
	 else { $starte = 1; }
	}
}
$zeilen++;
$ende = vorkommastellen($dividend);
schreibezahlintabelle( $rest, 0, $zeilen, $ende );
lesetabellenzeile( $zeilen, $stellengesamt );
tabellenfuss();
}

1.4 Anwendung des Programms

Das gesamte Skript kann man nun wie folgt nutzen. Man übergibt an adam-ries.pl eine Datei in der die folgenden Befehle enthalten sind.

div 829,0,3,0

Dabei ist eine Zahl immer in der Darstellung Zahl,Exponent.

1.5 Noch zu verbessern

Bisher funktionieren meine Programme einwandfrei mit ganzen natürlichen Zahlen. Aus Zeitmangel habe ich noch nicht Dezimalzahlen zur Genüge implementiert. Der Ansatz ist bereits vorhanden, dass man eine Zahl als Tupel angibt mit ihrem Exponenten. So ist z.B. 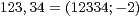. Aber dies wird nicht bei jeder Rechenart berücksichtigt. Bei der Addition und Subtraktion habe ich noch keine Ausrichtung an dem Komma eingebaut. Bei der Multiplikation und Division funktioniert dies bereits mit Dezimalzahlen. Als weitere Ergänzung ist noch eine Division mit Rest als Dezimalschreibweise gedacht. Bisher wird nur der Rest ausgegeben.

Literatur

[Bronštejn . Semendjaev, 1985]: Bronštejn, Il’ja . K. A. Semendjaev (1985). Taschenbuch der Mathematik. Teubner [u.a.], Leipzig [u.a.], 22 .
[Div., 2010a]: Div. (2010a). Addition. http://de.wikipedia.org/wiki/Addition.
[Div., 2010b]: Div. (2010b). Division. http://de.wikipedia.org/wiki/Division.
[Div., 2010c]: Div. (2010c). Multiplikation. http://de.wikipedia.org/wiki/Multiplikation.
[Div., 2010d]: Div. (2010d). Subtraktion. http://de.wikipedia.org/wiki/Subtraktion.
[Lergenmüller . Schmidt, 2004]: Lergenmüller, Arno . G. Schmidt (2004). Mathematik Neue Wege 5. Schülerband. Niedersachsen: Arbeitsbuch für Gymnasien. Schroedel, 1. .

Letzte Änderung: 07.07.2015: 21:33:26 von X. Rendtel

Dieses Werk bzw. Inhalt steht unter einer Creative Commons Namensnennung-Weitergabe unter gleichen Bedingungen 3.0 Unported Lizenz.
Beruht auf einem Inhalt unter www.rendtel.de.